The testing of a task went horribly right.
Background:
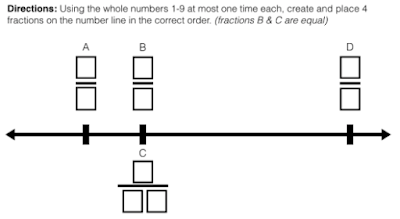
Graham Fletcher (@gfletchy) tweeted an Open Middle (@OpenMiddle) prompt for comparing fractions.
The thread debated whether or not a representation on a number line would be best.
Many people liked the number line better, but I decided to stick with the inequality signs because:
- Students see this type of two-bounded inequality notation with domain and range.
- The number line gave the impression of a single, fixed answer (because the fractions appear a definite, scaled distance away from each other).
I gave this question as a starter to a group of my grade nine students. They completed it in their portfolios.
Brief Summary of Action:
It is very hard to follow all student strategy without some type of documentation, but as far as I could tell, most of the student strategy followed two scaffolds.
- Start with the (open) middle
These groups began by focusing on the five digits necessary to fill in the equality in the middle of the prompt. Many centered their action around equivalent fractions to one-half. This actually prompted a shift in the reasoning to what was impossible rather than what was possible. One student noticed that if you chose one-half, you could not use two-fourths because the two had already been used. Another pointed out that this was doubly bad because none of the numbers were two digits. This triggered their group to create a list of other impossibilities. One-fifth proved to be particularly useless. Two-tenths, three-fifteenths, and five-twenty-fifths were all ruled out.
This action continued until the group settled on one of the possibilities. There was little debate about whether the choices made were correct, because almost every group acted as though multiple solutions were possible. (This is one of the strengths of the problem; it places students in an investigative stance). After the middle was chosen, the students created the two boundary fractions and compared sizes with common denominators or a variety of other estimation techniques.
- Set wide benchmarks
This subsection of the class was much smaller in size. They decided that the best way to ensure success was to create a really large fraction on the left and a really small fraction on the right. The problem would then be solved if the remaining five numbers could be written as an equivalent pair of fractions. These conversations were very fruitful as well. After hearing their strategy, I countered with the question, “How can you make a fraction as large as possible?”
The answers generally organized themselves around one of two possibilities: one-ninth and eight-halves or the reciprocal. Then the groups listed out the remaining middle digits and attempted to create an equivalent relationship (all the time confident that it would fall within the set range). If they couldn’t find one, they swapped out a single digit, and re-doubled their efforts.
Probably the best conversation of the day came when I challenged the fact that one-ninth was the smallest possible fraction. (Even if there was a fraction with a double digit denominator).
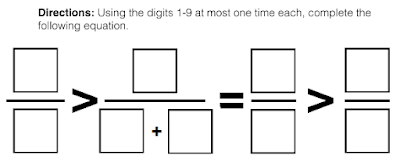
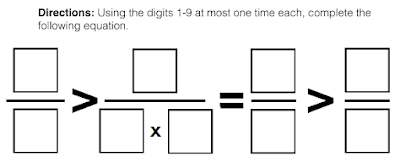
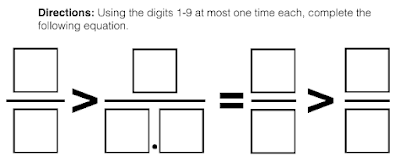
New Problems Posed:
I knew this task was going to provide conversation, but many of those conversations also posed new problems. Nothing out of left-field, but great problems because they 1) were simple and elegant alterations and 2) required a serious re-evaluation of the original strategy.
Here are three:
Needless to say, what was planned as a ten minute opener to initiate classroom inter-action ballooned into a period long buzz of reasoning, argument, justification, and re-posing. That, for me, is a beta test gone horribly right.
NatBanting
5 replies on “Fraction Task Testing”
I *love* this. I have many college students who struggle with fractions. THis is a perfect way to get them thinking…
Thanks for Sharing Nat! I really like the modifications you've made here at the end. Simple changes that provide a powerful product. I be using for sure!
What an awesome write up! I love when I get to peak inside a classroom, especially when an OpenMiddle problem is used. 🙂 thanks for sharing your insights and your class!
Great write up and love that it was done with 9th graders who I predict have mixed levels with fractions. I like the 2 divergent approaches that were each systematic in their own way. Great implementation. Kind of like when you do a 3 act and kids are engaged and getting it.
Thanks All!
It is difficult to describe dense mathematical action, but I hope I did it some justice. I especially like the denial point extension. Got into some very powerful conversations about place value and divisibility.