Surface area is intuitive. Intuition is a natural hook into curiosity. When you think something might (or should) be the case, it begs the question, why? It just seems as though textbooks haven’t gotten wind of that.
Perusing the surface area chapter of the assigned textbook for my Grade 9 math class offers a steady diet of colourful geometric solids all mashed together (at convenient right angles) in various arrangements. Without fail, the questions ask the same thing:
Find the surface area of…
Best case, students are asked to “create” a mimicked amalgam of standard solids and then calculate the surface area of their creation. Almost no mathematical decisions are made in the process of the creation. The question may as well read:
Do something random, and then follow strict procedures to arrive at a meaningless calculation.
I would like to afford students the opportunity to make meaningful mathematical decisions. That doesn’t mean the questions have to be exotic or complicated, but chances are they don’t involve trying to convince a teenager that they need exact calculations in order to purchase paint for their next re-modeling.
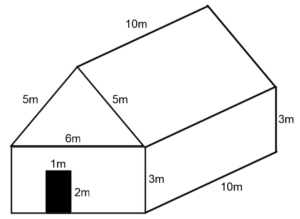
Here is my favourite surface area question ever (and I took it from a textbook*)…
…and here is what I ask the students to do…
*Actually, textbooks are a great starting place for inspiration.
The remaining attributes of good problems emerge out of a combination of 1) an eye for meaningful mathematical action and 2) teacher curiosity. (I mean, we want our students to be curious. The least we can do is be curious ourselves).
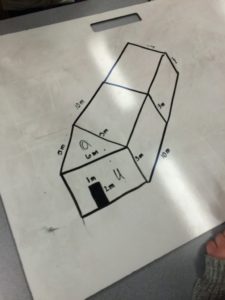 |
| The “back-to-front” design |
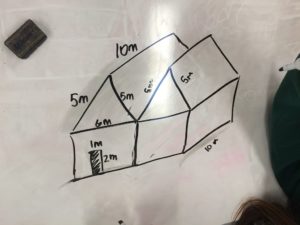 |
| The “side-by-side” design |
I think both of these are logical steps, and contain beautiful mathematical reasoning. It also uncovers a key understanding to surface areas and their overlap. What area is actually lost when the surfaces touch?
Most groups try to compensate by building additions to the existing structures of various levels of difficulty; most typical is the “accordion” strategy. This is where students push and pull the expansion (like a prism) until the surface area matches their goal.
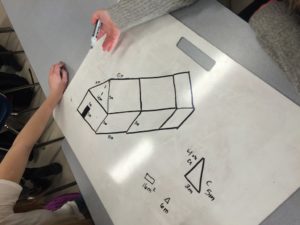 |
| The “accordion” strategy |
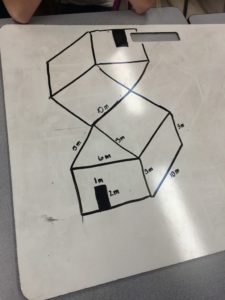 |
| Creative. Correct. Didn’t follow ALL instructions. |
I’ve had students overlap and then design balconies. I’ve had some punch enough windows to compensate. I’ve had groups append random hallways. This group got more than they bargained for with this elaborate and realistic solution.
 |
| Student design before dimensions are added. |
3 replies on “Double House Task”
Love this and can’t wait to try it with my Math Support Class. Thank you for sharing all of the details. Super cool. AZ
More upside down houses, please!
This is a brilliant idea, my students will love this! Friday Fun Day for maths.