My Grade 9 students don’t see an equation for the first two weeks of their unit of solving linear equations. That is because I think students get all bogged down in the notation, and lose their problem solving intuition.
Instead, I play around with a key metaphor for solving linear equations–the balance scale.
I’ve used the metaphor before, but only verbally alongside an algebraic representation. I would say things like, “What you do to one side, you must do to the other”, or “What would we have to do to keep the scales balanced?” The whole time, I only referenced the metaphor; students were never required to work with it. In hindsight, this probably did little to help students with the abstract nature of variable quantities.
Now, I get students to encounter a balance problem, and talk me through their solution. They begin to talk about things like “splitting weight evenly” when two circles are balanced against a value of twenty. They tell me that I can ignore a shape that appears on both sides of a balanced set of scales. The explanations come from them, and they encounter them through the lens of their everyday.
The abstract will come. Until then, students encounter various principles of equations as different sets of scales are presented.
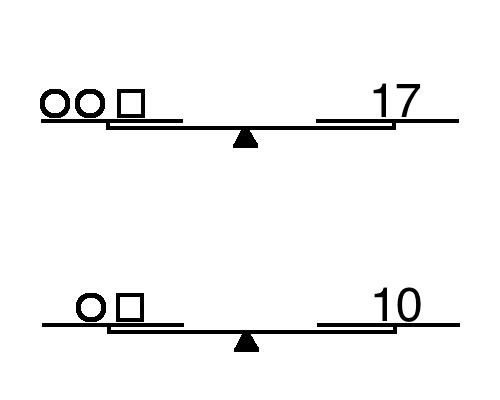
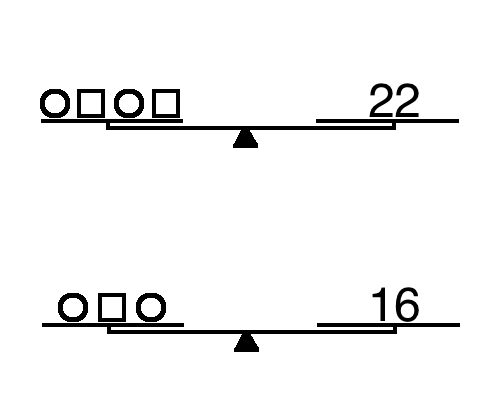
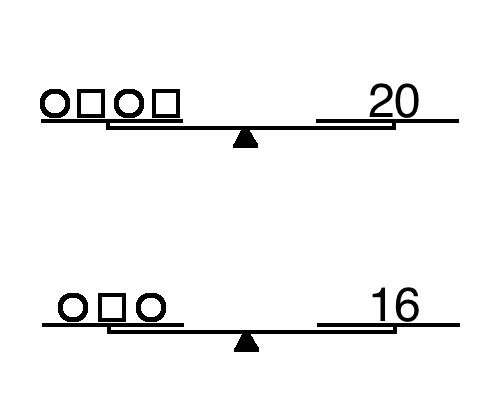
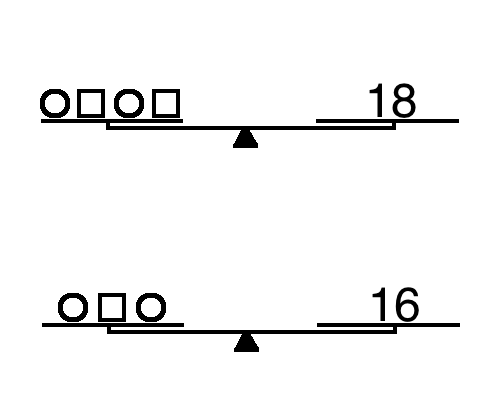
Below are nine sets of scales to introduce the notion of systems of equations. Teachers–and textbooks–talk about “real world” as a way to tether topics to students, but I have always had trouble finding a task that can make the conceptual leap from the situation (phone plans, car trips at different speeds, etc.) to the algebraic notation.
Instead of appealing to the students’ surroundings, these scales are “real” in the sense that they appeal to their intuitions–their unavoidable tendency to organize, categorize, and achieve balance.
Each question consists of two sets of scales, and students must find the weights of the circle and square. The nine questions are divided into three sets with small variations included. The three are designed to be used as a single object (Watson & Mason, 2006). This is done with the hope that students will use these small shifts to build a better understanding of how the variables act on one another.
They are relatively simple to create. Obvious extensions include fractions of circles and squares as well as more “variables” (shapes). Any typical textbook exercise can be converted quite easily. Having these pairings (or having students create them) can be a powerful tool.
Set 1




2 replies on “Visualizing Linear Systems”
Check out "Transition to Algebra". I'm not sure if the entire text is published yet but there are many excerpts on the site. The book employs mobiles similarly with the intuitive concept of balancing – really helped my algebra enrichment class last year. Might give you some ideas!
I love the idea of developing students intuition, and tying it to the math. I've found that kids have a resistance to the concepts unless they can relate it to something real. Once they can relate or visualize it, they can understand the rest. I recently built a fractions learning app to develop that intuitive understanding of fractional amounts – http://infinut.com/fractions-by-infinut/. As a result, my 8 year old learnt how to add, sub, equivalent, div fractions. It was quite amazing to see her math understanding develop. Would love to hear your thoughts on it too.