Introduction
This page is dedicated to the conjecture that modelling work doesn’t need to take place in a context. What’s important is the direction of the work: that it asks students to build a model to specifications before turning around and employing the model to solve for unknowns. The activity of designing custom models to fit specific constraints is what I term “Upstream Thinking,” and this design process fits quite nicely in our algebraic-minded courses if we use task structures that encourage students to make a high number of design decisions and analyze the fallout from said decisions. Here, you will find lists of constraints that pertain to specific types of functions you and your class may be studying. They are the building blocks for three types of contextless modelling tasks that I have used with my students: boxes tasks, wanted tasks, and menu tasks. Each type of task is described below. The hope is you use the lists of constraints to design tasks of these types to encourage students to build custom models to specifications–to think upstream. (These lists are a starting point; please get creative and feel free to pass along any inventions!)
Boxes Task
A boxes task takes the parameters of the equation of a function and replaces them with empty boxes. The students are then asked to fill in the boxes with values to satisfy a set of constraints (Typically 3-4 constraints are given to the learners all at once). The numbers available for entry into boxes can be restricted to sponsor further thinking. (This type of problem has become popularized by the work of openmiddle.com).
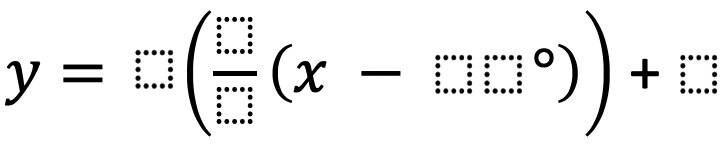
Wanted Task
A wanted task (name inspired by Chris Hunter) asks students to build and shift the design of a model as a list of constraints is released one at a time. After each constraint, students need to verify that their current model satisfies the new constraint, or alter their function to meet this new requirement. The model is appropriate if it satisfies every constraint. Teachers can pre-sequence a list of constraints or choose them randomly–but this makes it more likely that a model satisfying each constraint is impossible to build. This is an important conversation, but impossibility is not the ideal result for every wanted task. Examples of wanted tasks asking for quadratic models can be found in this post.
Menu Task
A menu task gives students a longer list of constraints (around 8-10) and asks them to build as many functions as necessary so that each constraint is satisfied with at least one of their custom functions. There is no restrictions for the values of the parameters, and all the menu’s constraints are given at once. Rich opportunity arises as students attempt to resolve the menu with as few functions as possible. They begin to analyze which constraints pair well together and which cannot pair together. A more detailed rationale can be read in this post, and a complete set of the online community’s submission is crated on this site under #MenuMath tab.
Linear Functions
| Positive y-intercept | Negative y-intercept | Slope of -2 |
| Positive x-intercept | Negative x-intercept | Slope of one half |
| Never enters QI | Never enters QIV | Never enters QIII |
| Goes through the point (-5 , 6) | Goes through the origin | Never enters QII |
| Slope greater than 3/2 | Slope less than 1 | Touches both axes at integer coordinates |
| Has a fractional slope value | Increases faster than y=-2x + 1 | Increases slower than y=1x - 2 |
*sample of a linear menu (from Amie Albrecht)
Quadratic Functions
| Has a vertex in quadrant I | Opens up | Opens down |
| Has a vertex in quadrant III | Has a maximum value | Has a minimum value |
| Has a vertex on the x-axis | Positive y-intercept | Two x-intercepts |
| Has a vertex on the y-axis | Negative y-intercept | No x-intercepts |
| Goes through the point (2 , -3) | Never enters QII | Two negative x-intercepts |
| Horizontally stretched | Never enters QIV | Two positive x-intercepts |
| Vertically stretched | Contains points in all four quadrants | Axis of symmetry in Q I & IV |
*sample of a quadratic menu (from yours truly)
Polynomial Functions
| Has 2 turning points | Has no turning points | Has 2 x-intercepts |
| All x-intercepts are positive | Has an even degree | Has an odd degree |
| Never enters QIV | Never enters QII | Has more turning points than x-intercepts |
| Ends in QI | Ends in QIV | Starts in QII |
| Starts in QIII | Goes through (3 , 5) | Has a bounded range |
| Always increasing | Always increasing in QI | Has an infinite range |
| Has more x-intercepts than y-intercepts | Has a turning point on the x-axis | Has a y-intercept at the origin |
Exponential Functions
| Is increasing | Is decreasing | Has a negative x-intercept |
| Has a positive x-intercept | Has a negative y-intercept | Has a positive y-intercept |
| Has no x-intercepts | Has a base > 2 | Has a base < 1 |
| Goes through the point (2 , 3) | Goes through the point (2, 1/2) | Goes through the origin |
| Intercepts the y-axis at a fractional value | Never enters quadrant I | Never enters quadrant II |
*sample of an exponential menu (from Sheri Walker & Tania Asselstine)
Sinusoidal Functions
| Has an amplitude of 3 | Has a midline above the x-axis | Has a midline below the x-axis |
| Never enters QIII | Never enters QII | Has a period length greater than 2π |
| Has a y-intercept at a maximum value | Has a y-intercept at a minimum value | Has a period length less than π |
| Is non-symmetric about the x-axis | Is symmetric about the y-axis | Has a max value at (π/2, 4) |
| Is phase shifted to the left | Goes through the point (2π, 0) | Is phase shifted more than one period length |
*sample of a sinusoidal menu (from Dylan Kane)
Rational Functions
| Has a vertical asymptote in QI & QIV | Has a horizontal asymptote in QI & Q2 | Has a vertical asymptote in QII & QIII |
| Has 2 vertical asymptotes | Numerator has a degree of 3 | Has a vertical asymptote in QI & QIV |
| Never touches either axis | Has an x-intercept at (4 , 0) | Denominator has a degree of 2 |
| Has a positive y-intercept | Never enters quadrant III | Has 3 x-intercepts |
| The degree of the denominator is greater than the degree of the numerator | The degrees of the numerator and denominator are identical | Has a negative y-intercept |
Functions (General)
| Goes through (3 , 4) | Horizontal asymptote in QI & QII | Negative y-intercept |
| Goes through (-1 , 2) | Never enters quadrant I | Positive y-intercept |
| Vertical asymptote in QII & QIII | Never enters quadrant II | Has more x-intercepts than y-intercepts |
| Vertical asymptote in QI & QIV | Never enters quadrant III | Negative x-intercept |
| Passes through the origin | Never enters quadrant IV | Positive x-intercept |
| Has a minimum value | Has a maximum value | Never decreasing |
| Has an infinite range | Symmetric about the y-axis | Never increasing |
Calculus
| Has a relative maximum in QI | Has 3 critical points | Has a vertical asymptote |
| Has a single x-intercept | Is not differentiable across its domain | Is not continuous across its domain |
| Has a positive y-intercept | Has a negative y-intercept | Is always decreasing in quadrant II |
| Never enters QI | Has at least two points of inflection | Has an inflection point in QIV |
| Has a local minimum in QII | Goes through the point (3, 5) | Its y-intercept is a critical point |
*sample of a calculus functions menu (from Erick Lee)