My fascination with infinity began early on in life. I went to a small private school in Prince Edward Island for my entire elementary school career, and it was outside on the playground where I first tasted the enigma of infinity and the power it held.
Across the cul-de-sac parking lot stood the swings, slide, and monkey bars; I still remember the first time I encountered infinity under those bars. You see, we had been learning the base-10 number system that day, and my friend Jason and I somehow got into a counting contest of sorts. We began at very small numbers, and gradually cycled through the digits at varying positions until we countered each other with unusually large–and most likely inaccurate–numbers. Trillion, Quadrillion, Bazillion all made appearances until Jason ended the contest with one word–infinity.
I countered with infinity plus one, but was quickly informed that infinity plus one was equal to infinity. Despite my protests, his knowledge won out. Every number seemed to be imbibed into infinity; I had lost the contest. Needless to say, I initiated many other counting contests shortly thereafter. It seemed that no middle school student was willing to fight with infinity.
After Buzz Lightyear popularized infinity in the media with his classic catch phrase, it is the most common response I get from students when I ask for their thoughts on infinity. I have inserted tidbits on the subject throughout this semester to get students thinking about a horribly inhuman topic.
Humans are built on limits; we all have boundaries. Infinity can’t occur because we are not infinite. Like today–it was my birthday; I turned 24. I told my students that yesterday my age was prime, and next year it will be a perfect square. From this information, they guessed correctly that I was 24. I asked them if there were any more possibilities.
Three, Eight, Forty-Eight, Eighty…
I then asked them if they thought that there were an infinite amount of numbers that fit the pattern. Human sense had limited them to really 2 answers (24 and 48), but when I moved them into infinity they reluctantly thought there must be an infinite number of possible ages. I introduced them to the concept of a prime twin, and the open problem that has plagued mathematicians for years.
A prime twin is a set of two primes that differ by 2.
eg. 3,5
5,7
11,13
It seems likely, but has not been proven. We can, however, prove that there are an infinite number of primes. This short dip into the infinite led back into our studies of primes, factors, and GCFs.
The coolest application of infinity (outside of limits) in our curriculum is infinite geometric series. If I have a fixed distance, and step across exactly half of the remaining distance with each subsequent step, I will get to the other side–if I take infinity steps. How can this be? Won’t there always be a little space?
Some tinkering with fractions revealed a new angle. Stepping 1/4 of the way with each step would get me 1/3 of the way across. Mathematically, we say the series converges to 1/3. Such an analogy can be represented in the image below. Shading 1/4 of a square, then 1/4 of 1/4… etc. Iterating an infinite number of times yields an area of 1/3 square units.
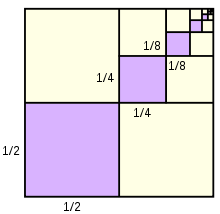
That reminded me of another problem from my youth. My grade 10 math teacher once asked us to trisect an angle. After many attempts and trials, I gave up. I could get close but could never prove it geometrically. That was before I had the power of infinity. It is easy to bisect an angle, so any angle can be quickly divided into quarters. Shade one of the quarters and then bisect the adjacent quarter twice to create 1/16 of the original angle. Shade that adjacent 1/16 and then bisect accordingly until the 1/16 is now a 1/64. Doing this an infinite amount of times would yield a trisection of the angle because the sum of the infinite series converges to 1/3. After I had this idea, I researched to find many other ingenious ways people have skirted the original problem.
It seems ridiculous to continue the shading into infinity; can it even be done? These are great questions for students. Rather than letting the mathematical notation take over, allow the students to grapple with the implications of infinity. Students will be defiant that there is no way to actually reach infinity, so telling them that the formula does reach infinity may ruin that adventurous and discerning spirit. Pose problems, change parameters, and allow infinity’s enigmatic persona fascinate your students much like my first experience under the monkey bars.
NatBanting
Humans are built on limits; we all have boundaries. Infinity can’t occur because we are not infinite. Like today–it was my birthday; I turned 24. I told my students that yesterday my age was prime, and next year it will be a perfect square. From this information, they guessed correctly that I was 24. I asked them if there were any more possibilities.