Exactly one month ago, fellow Saskatchewan mathematics teacher Ilona Vashchyshyn tweeted about an area task that she used in her class. Long story short, it captured the imagination of Math Ed Twitter like elegant tasks have a tendency of doing.
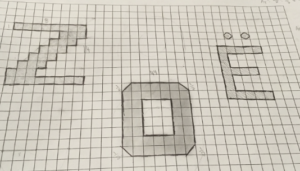
The challenge: Write your name so that it covers an area of exactly 100 cm squared.
Love the different strategies students used here. E.g. Leia, who chose to make each letter 25 cm^2. Notice the revisions on the A.#mathchat #MTBoS Cc @PaiMath pic.twitter.com/FowEQoL4I6
— Ilona Vashchyshyn (@vaslona) November 16, 2018
Two weeks later, my grade 9s and I were beginning a unit on surface area and this seemed like a perfect entry point. I thought it would provide a perfect window into what geometric knowledge they were bringing with them into the unit. Because my crew would be dealing with the surface area of a cylinder, I altered the task slightly:
Write your name so that it covers an area between 99 and 100 cm squared.
*you must include at least one rectangle, one triangle, and one circle in your design.
Student work:
The results were as creative as expected. The task seems to encourage a commitment to symmetry with many students calculating a sort of square budget for each letter of their names or making all letters uniform in height. Also, their attention was immediately drawn to the shape of most resistance–the circle. There was almost an immediate recognition that rectangles and triangles live nicely on a grid, but circles do not. This became an important talking point throughout their work.
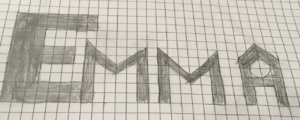
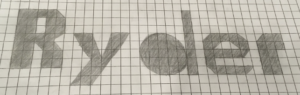
Beyond the products:
As the students worked, three important themes came out of our conversations. These pieces of intel gave me a sense of where we were collectively strong and where more connections were needed.
1. Unearthing of vocabulary
The task provided plenty of opportunity to talk about the vocabulary associated with area. Words like dimension, formula, area, radius, diameter, base, height, and squared were all discussed. I really like introductory tasks that provide opportunities to acclimatize to the verbiage while content demands remain relatively low.
2. Connecting counting to calculating
The grid encourages students to count squares in order to tally their total square area. While this is a nice connection between the idea of shaded squares and square units of area, I was interested if the students could also assign dimensions to shapes and calculate their area with appropriate formulae. Requiring them to incorporate a circle made calculation a necessity, but also provided the opportunity to connect this back to counting.
After having several conversations with students about the link between counting and calculating, I asked some students to put their work under the document camera. My set-up is an iPevo VZ-R, which allows me to clearly project and zoom in on sections of student work. The camera has all kinds of functionality, but I have found it most useful in my classroom as a tool for sharing ideas. (I often “pause” activity half way to discuss strategies that are emerging in the classroom).



As a class, we focused on the ways that students had incorporated the circles. We then calculated their area with the formula and compared with a counting strategy to check their correlation. This exercise helped students add meaning to the calculations that (I knew) would dominate much of their activity in the unit.
3. Practicing sub-sectioning and calculating
We started outlining the dimensions of the shapes we were viewing under the document camera. It didn’t take long for students to see the compound calculations in different ways. For instance, the “L” in “Laurier” can be divided into a 6×1 rectangle and a 1×3 rectangle. Alternatively, it can be dissected into a 5×1 rectangle and a 1×4 rectangle. This slicing of compound shapes into more familiar ones is a critical skill when calculating surface area. One student suggested that we could calculate the area of the “A” in “Laurier” by tracing a 6×5 rectangle around the entire letter and then subtracting the triangles created “on either roof”. In the end, the class decided that this resulted in more work, but zooming in and tracing out the idea provided us the chance to discuss the possibility of multiple correct dissections.
___
I think the immediate appeal of the task (as evidenced by the sheer volume of social media activity) was in the beautiful creations of students. However, its value goes beyond what appears on the paper; the simple prompt is a powder keg for critical conversations about area.
NatBanting