I want students to solve systems out of necessity.
I want them to feel the interconnectedness of the two (or three) equations. In the past, I’ve asked small groups to build a functional 4×4 magic square. Soon they realize that changing a single number has multiple effects; this is the nature of the system. Unfortunately, abstracting the connections results in more than two variables. This year, I wanted to create the same feeling with only two variables. (The familiar x & y).
Enter: Alex Overwijk.
We blitzed through a task of his for systems of equations when I participated in a workshop of his last year. His blog is fantastic, because he recounts classroom events. It is filled with straightforward stimuli for the practicing teacher. His ideas have occasioned many tasks of my own.
I took his post, and extended it into inequalities.
Day 1: Equalities
I purposely chose a system that
- Didn’t use too many pennies
- Did not have a solution over the set of natural numbers
- Had 3-4 options of “close calls”
I settled on the following situation (directly from Alex’s post):
Two children go into the candy store. Bob buys 3 JuJubes and 4 Smarties for 26 cents. Sally buys 2 JuJubes and 7 Smarties for 24 cents. If every JuJube costs the same and every Smartie costs the same, what is the price of both candies?
They grabbed a handful of pennies and coloured tiles and got to work setting up the situation in much the same way Alex’s students did.
After 3-5 minutes, students started to get close to solutions, but they continued to evade them (by design). My conversations with the groups went something like this:
Me: What’s up?
Them: It doesn’t work?
Me: What doesn’t work?
Them: The prices. You can’t do it. There is some left over.
Me: Then increase the price.
Them: [adding pennies] but then this one doesn’t work.
Me: Then I guess take some away to make them match.
Them: But then we have too many…
…and it would continue on. They couldn’t make a move (change a price) in isolation. This is the feeling I wanted from the system–interconnectedness.
[One student asked if they could break the pennies up, and I said that thinking was interesting, but not possible. I planned on bringing that line of thought up after class discussion]
As the discussion of strategy began, the class quickly realized that no solutions existed (with these objects). Some began with high prices and then punched numbers in calculators in linear combinations until they matched. Others worked in tandem with one student calculating JuJube price and the other Smartie price. Some began with both candies being one cent, and then walked up until they reached the boundary. All contained great mathematical action, but none yielded a satisfactory answer.
I then began to alter the notation.
First, I defined JuJube to be “J” and Smartie to be “S“. Then re-wrote the equations.
3J + 4S = 26
2J + 7S = 24
Second, I replaced “J” with “x” and “S” with “y“.
3x + 4y = 26
2x + 7y = 24
Third, I numbered the equations.
(1) 3x + 4y = 26
(2) 2x + 7y = 24
At this point, several “ooooooohhhh” sounds came from the class. They had just finished solving systems of linear equations in grade 10. We then refreshed the vocabulary of this process and I gave them the next scenario (one with a nice solution). We ended the day talking, once again, about the interconnectedness of systems.
Day 2: Inequalities
I began the day by randomly grouping the students and placing a familiar problem on the board.
2 JuJubes and 2 Smarties cost 18 cents.
4 JuJubes and 3 Smarties cost 33 cents.
How much to JuJubes and Smarties cost?
They got to work arranging their pennies and quickly arrived at a solution of (6 , 3). I then posed a new scenario.
Two young gentlemen want to impress their girlfriends by giving them a dynamite Valentine’s gift. The first can spend up to 18 cents, and wants to buy his sweetheart 2 JuJubes and 2 Smarties. The second can spend up to 33 cents, and wants to get his sweetheart 4 JuJubes and 3 Smarties. What could the prices be so that both gentlemen can get their desired gifts while remaining under budget?
The take up was slow until one student suggested that they steal the candy. This was a great starting point because I told them they wouldn’t have to steal them if all the candy was free.
Him: “You can do that?”
Me: “Would that mean both gifts were bought under budget?”
Him: “Yes”
Me: “Then it seems to fit. Zero cents for a JuJube and zero cents for a Smartie is a possibility”
Then I asked groups to find all possibilities. I put them into a table in Desmos to show the pattern.
The result was a stippling pattern on the natural number solutions. This created a natural way to talk about the different domains and ranges that the problems require. I have never had such an organic entry into stippling; I always just said those were the spots that were “allowed” because of restrictions.
Day 3: Abstraction
On the third day, we went through examples of notation and mechanics of solving the problems. It was interesting to hear how many times a student would refer to candies or pennies when explaining things to other students.
My goal here is to mimic Alex’s style and provide you with a start–an actual account of how it ran in my classroom. You know your students best, and have a intuitive feel for when they need more scaffolding or higher ceilings. Take this, adapt it, and extend it further.
NatBanting
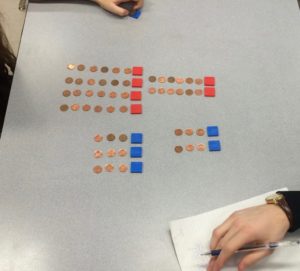



4 replies on “Candies, Pennies, and Inequalities”
Thanks for providing so much detail!! It really helps me picture how to recreate this with my students. I love the idea of grounding that idea of interconnectedness.
This is brilliant dude! Wish I could spend a day inside your head. 🤔
Hi,
I think you have an error in your numbers. In the first scenario, the solution does not work out to whole numbers unless both Bob and Sally’s costs are both 26, not 26 and 24. You also change 26 to 36 when relabeling the variables from J and S to X and Y.
Otherwise, great ideas.
Thanks
Hey!
Thanks for catching the “26” –> “36!
As for the whole numbers, that is the exact point. I gave them one that had them work with the mechanics of a system without ever settling on a solution (because they didn’t have the ability to break the objects).
Allowing them to arrive at a solution would cut the investigation short and stifle necessary conversations.
Thanks for reading!
Nat