I can’t–for the life of me–understand why someone would argue to eliminate high level mathematical reasoning in favour of memorized tricks, but that seems to be the case with those arguing against the Common Core State Standards. I cannot fathom how this can be the case except to chalk it up to a case of “he-said-she-said”. Change (especially in something as resistant to it as mathematics education) breeds ignorance. And Ignorance breeds fear.
Let’s face it: The public is scared of reform efforts and most teachers aren’t far behind.
There are multiple (legitimate) reasons.
- Time
- Mathematical Proficiency
- Control / Power
- Outside Testing Pressures
- Belief about University Requirements
- Personal Histories
the list goes on and on.
All of these things considered, I still find it impossible to figure out why a teacher would want to condemn the methods aimed at deep understanding. (Other than, of course, they haven’t taken the time to see what it is all about).
Some would say that the methods do not actually achieve the deep understanding they claim to, but I would caution them (alongside Dewey, 1938) to tread lightly if they believe they can control what anyone learns at any time. Learning is a complex process that is not prescribed; claiming that it is optimal to internalize a ‘canon’ of ‘truth’ exactly as it is presented is one assertion, but assuming that such a feat is possible is something much larger. (In my mind, ignorant).
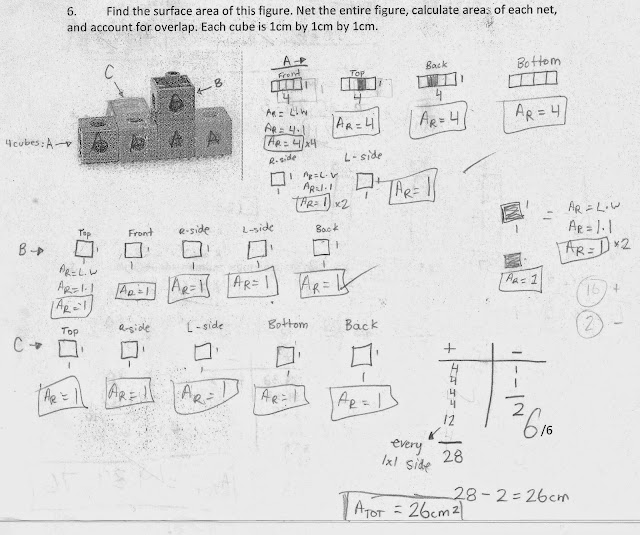
With this incredibly provocative preamble behind us, let’s take a look at what sparked this thought. A series of four responses (many more were worthy of exposure) to a typical question on surface area in my Grade 9 regular stream classroom. Each student “received” the same educational experiences, but came up with different ways of conceptualizing the task. People may dismiss this as fluke or ignore it all together, that is your prerogative.
Just know:
- This is real. It is not fabricated. It is not doctored. The scans were simply cropped by myself to ensure complete anonymity.
- This unit didn’t take more time than usual. I didn’t spend a thousand hours allowing for “aimless” exploration.
- I didn’t prescribe what method to use, but encouraged discussions on efficiency. It wasn’t an “everything goes” culture; strategies were analyzed.
- The students generated each one of these in consultation with their peers, histories, and classroom experiences.
If you choose to ignore the possibilities (albeit from a very concrete, accessible topic), fine. But if you care to do so by intelligent and sophisticated means, please tell me why students using these strategies is a detriment to them, their future, and the education system.
One last appeasement. Even if one believes that right answers and streamlined edges are the purpose of mathematics (**cough** which they are certainly not **cough**), each of these arrives at the correct answer. This is a nice precipitate come exam time, but certainly wasn’t the case during concept development. The mistakes were culture forming; they encouraged reflection and recursion–not something to be shunned. Some of the strategies even looked somewhat “standard” **gasp**
Without further ado, the question and four responses:
References:
Dewey, J. (1938). Logic: A theory of inquiry. New York, NY: H. Holt & Co.