I have students in an enriched class that demand for me to give them more practice. I tell them that we practice mathematics with daily class activities. They don’t want practice, they want repeated practice. They are accustomed to receiving repeatable drills to cement understandings.
I have learned to compromise with this demand. I do believe there is a place for basic skills training in mathematics, and would raise an eyebrow at anyone who claims these unnecessary. I do, however, also believe that the heart of mathematics is problem posing, problem framing, and problem solving.
Here is how I’ve infused an ounce of conceptualization into regular drills. (I use this for both practice in a large group discussion, small group rotation format, take home work, as well as unit exams.)
The work begins like many math classrooms with a set of problems to do. In this post, the topic at hand is solving equations (at the Grade 9 level).
I’ll give ten or so to show the possible variety in structures, and then begin to ask questions that allow students to think deeper about the rules they just employed. Most of these questions focus on flexible use and mathematical communication.
Here’s a question from my most recent unit exam on solving equations:
The question then reads:
Fill in the blank with the number that makes this equation as simple as possible. Explain your choice.
Once you’ve explained your choice, go ahead and solve the equation. Show all work.
The results were fantastic. It was excellent for me, as a teacher worried in skill development as well as deep, conceptual growth, to see that these students were grappling on a deep level with the content when probed to do so. I was assuming that many students might choose “3” to match the denominators on the left-hand side. This scared me, because I felt that I was baiting my students into mistakes. Turns out, not a single student responded with “3”. The most popular responses were “2” (foreseeing the first inverse operation), “6” (choosing a LCM of all denominators present), “5” (fully simplifying the fifths), and “1” (assuming that eliminating fractions is always easiest).
Great insight.
The exam questions are a nice break from traditional assessment while still affording the convenience and balance of a pencil and paper test. My favourite format for these conceptual drills is a small group jigsaw where each group answers, explains, and rationalizes their actions to the larger group. It sparks great discussion.
Here’s a question used in the unit on solving equations:
The question then reads:
Change a single digit from the equation above to make the problem as simple as possible. Explain why you made the choice, and then proceed to solve the equation. Show all work.
Popular choices include changing the “2” to a “1” and shifting the “5” to a “6”. These moves both have ample justification and spark great conversations. Eventually the topic of fractions came up, and students said that they would like to avoid them altogether. That led me to the natural extension:
Is there a number that we can replace “2” with to avoid fractions altogether? How many of these numbers exist? How can we find them?
The discussion skyrocketed from there.
It causes me pause to think about why discussions like these don’t happen more often. Is it a time issue? Do teachers see them as wastes of time? Do teachers struggle with the dimensions of problem posing necessary to see beautiful math staring them right in the face? Is it downright confusion of the purpose of mathematics?
**TANGENT: I think teachers don’t practice looking for mathematics. We waste our time trying to appear mathematical by partaking in various stereotypical mathematical whimsies such as an undue infatuation with Pi day and the obligatory kudos to binary clocks. There is more to mathematics than surface niceties.
It is one thing to preach balance but to continually teach at the poles. One day we work on a task and “construct” mathematical knowledge, and the next we “lecture” and “practice”. Learning doesn’t operate on this notion of average–flip-flopping will only confuse students. We need to develop a curriculum and supporting pedagogy that lives between the two worlds at the same time. Procedural and conceptual are not nearly as mutually exclusive as they are mutually dependent.
NatBanting
PS. For another foray into this conceptualizing of drills see David Coffey’s worksheet adaptation.
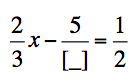
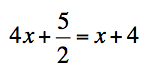
6 replies on “Conceptualizing Drills”
This is the coolest way to get kids to write and think critically. I love the way you have taken normal problems and changed them to supercharged problems. Thanks for sharing.
Delightful change to the standard 'drill' problems. Thanks much for sharing!
Very elegant. I admire the mathematical thinking and expressing you are inspiring in your students. I'd like to see examples of a similar structure used with students with lower math skills (Less math skills than 9th grade algebra) Is there anywhere you'd suggest that I look?
@abby
First off, thanks for reading. These skills are definitely not reserved for the high school level. In fact, I think they are better suited for younger students. As far as a place to look for examples, I would say try looking… within. (corny, I know)
So much of problem posing is fluid, and showing you examples or fabricating examples will only satisfy you for a small time. This post (hopefully) provided the impetus for you to try conceptualizing drills. In my attempt to teach you to fish, I needed to include a couple frozen fish fillets so to speak.
Here is an example from a conversation with a grade 4 student today. I asked how many weeks were in a year, and he only knew the days. He then said we could divide 365 by 7 to get our answer. He soon discovered this would be very difficult, so I asked him, "What numbers do you know that would be easy to divide by 7?"
This is a great starting point to a conceptualization of division and multiplication (and its link to addition). Could also even abstract distribution.
The point is, you have the power to shift a drill by posing problems. The framework of "make this easier" is just one I've found to be particularly effective because every student has a different connotation of "easiest".
Thanks for reading, I hope this helped.
Nat
First, as I try to solve this myself, is there a missing 'x' in the first question? Or, quite possibly, I am missing something.
Thanks for sharing this example. Love it! Were there any kids that didn't engage or try these? If so, what did you do to support them?
@ccampbel14.com
There is not a missing "x". Although, I see an opportunity for an interesting extension. If the blank was to become an "x", how would you solve that problem? The initial equation was intended to look at the effects of rationals in equations. I only included one unknown so that goal was focused.
There are always a few students that do not engage in any activity. This cannot be a deterrent to change. More students attempted this problem because it gave them an opportunity to effect their work. That ownership is powerful. If students do not attempt, I try to engage them unobtrusively. As someone explains their choice, I might ask them if they have anything to add, or if they agree. I think teachers know how to support their students; use that relationship to know how each student can be pushed.
The nice part of this is that this activity can fit seamlessly into a classroom and begin to get students thinking conceptually.
Thanks for reading.