Double House Task

Surface area is intuitive. Intuition is a natural hook into curiosity. When you think something might (or should) be the case, it begs the question, why? It just seems as though textbooks haven’t gotten wind of that.

Perusing the surface area chapter of the assigned textbook for my Grade 9 math class offers a steady diet of colourful geometric solids all mashed together (at convenient right angles) in various arrangements. Without fail, the questions ask the same thing:

Find the surface area of…

Best case, students are asked to “create” a mimicked amalgam of standard solids and then calculate the surface area of their creation. Almost no mathematical decisions are made in the process of the creation. The question may as well read:

Do something random, and then follow strict procedures to arrive at a meaningless calculation.

I would like to afford students the opportunity to make meaningful mathematical decisions. That doesn’t mean the questions have to be exotic or complicated, but chances are they don’t involve trying to convince a teenager that they need exact calculations in order to purchase paint for their next re-modeling.

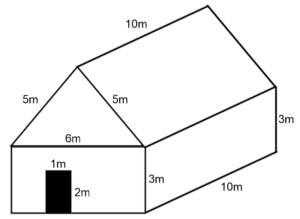
Here is my favourite surface area question ever (and I took it from a textbook*)…

…and here is what I ask the students to do…

Design an expansion for this house that doubles its surface area. The expansion must share some portion of a wall with the original house.

*Actually, textbooks are a great starting place for inspiration.
The remaining attributes of good problems emerge out of a combination of 1) an eye for meaningful mathematical action and 2) teacher curiosity. (I mean, we want our students to be curious. The least we can do is be curious ourselves).

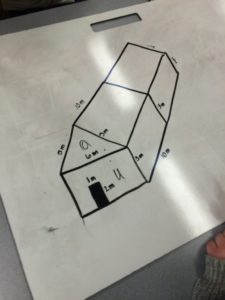I group them randomly into 3s and give them a large whiteboard to work on. The results begin predictable, but the avenues for re-calibration of their actions are incredible. They quickly discover that the problem is not so simple.

Most groups start one of two ways:

The “back-to-front” design

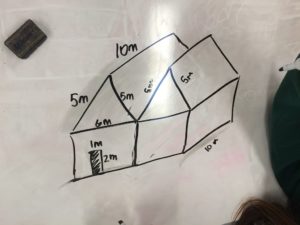The “side-by-side” design

I think both of these are logical steps, and contain beautiful mathematical reasoning. It also uncovers a key understanding to surface areas and their overlap. What area is actually lost when the surfaces touch?

Most groups try to compensate by building additions to the existing structures of various levels of difficulty; most typical is the “accordion” strategy. This is where students push and pull the expansion (like a prism) until the surface area matches their goal.

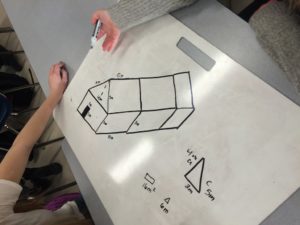The “accordion” strategy

Again, this is filled with wonderful mathematical thinking. Watching a side-by-side group accordion is particularly interesting. Do they pull out both sides? or just one? Do you include the roof? or just pull out a rectangular prism?

The problem would be cool if the thinking stopped there, but it never does. If you give the student space and an intuitive problem on which to act, you will get super cool alternatives that are not necessarily practical in terms of actual building design. But in math class, they represent brilliance.

Take this group’s Escher-like solution of balancing the house together. Their justification was, “We are not bound by the laws of Physics”. I asked if these two houses shared a wall, and they reluctantly re-organized their design. What they didn’t do was slide the roofs together a little. This surprised me.

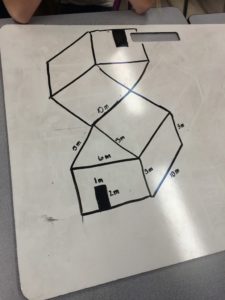Creative. Correct. Didn’t follow ALL instructions.

I’ve had students overlap and then design balconies. I’ve had some punch enough windows to compensate. I’ve had groups append random hallways. This group got more than they bargained for with this elaborate and realistic solution.

Student design before dimensions are added.

Surrounding all of these results is the sphere of possible actions. Most of the actions are based around the strategy “overlap an entire wall, and then compensate for the loss”. Very few act on the strategy “overlap a small portion of a wall and make a small alteration”. Sometimes I ask them why they overlapped so much, and they usually respond that it is easier to work with larger numbers because surface area grows so fast. This is also a great noticing.

The procedure of finding surface area is embedded in all of this is. In that sense, the original instructions of “Find the surface area of…” are still there. They are just steeped in the possibility of student action. It is the simplicity of the intuitive hook that makes this my favourite surface area questions ever. Maybe that’s because I don’t know which strategy I like best.

NatBanting

3 replies on “Double House Task”

Leave a Reply Cancel reply