Estimating with InO-Bot

You can count me among the folk that believe that there is a real possibility to teach mathematics (among many other things) through coding. I do not claim to have any expertise in the area aside from a handful of undergraduate credits and the odd project that has grabbed my attention over the years; however, the intuitive nature of Scratch provides a novice entry point for anyone interested in giving it a shot. This post describes my initial foray into using coding technology in the classroom. Like all things, the structure of school provided certain constraints, but in the end, it was a very positive experiment for both myself and the students.

The project began when I was provided with two InO-Bots from Canadian Classroom¹. These Bluetooth Scratch robots come with their own set of commands that link with the Scratch programming language. The commands range from very simple (like forward and backward movement) to complex (like sensing obstacles or responding to volume levels). Like most programming languages², the scripts can be written as simple, linear progressions, or as more complex, interconnected programs. 

I had one major focus when designing an introductory activity for learners: I wanted the coding to support the math curriculum outcomes explicitly. That is, I did not want to teach math and coding, I wanted to teach math through coding. Because coding is not explicitly written as a part of our standards, there were a few strands I targeted, eventually settling on the measurement of lengths and angles.

I also only had two robots, so knew that whatever coding that was done would need to be done as a class. I needed a way to get students to work with the estimation of angles and lengths, but also needed a way to keep their attention while other groups of students were creating their code.

The Task:

We set up a classic obstacle course. These types of activities are popular with programmable robots. It keeps the commands simple (movement and turning), and also seemed to be appropriate for the estimation of angles. We taped out an ideal path with painting tape, and used a collection of abandoned classroom geometry tools to set up a series of obstacles that would interfere should the robot stray too far off course. We drew a diagram of the course on the front board, and also projected the Scratch coding platform from the tethered laptop.

The students were given two goals:

1. Get the InO-Bot as close to the finish spot as possible.
2. Stay as close as possible to the green line.

Originally, we planned to have each group estimate the course, code and test their estimations one at a time, and then take the average of everyone’s estimations to see if the path got more or less accurate. However, once the students began the task, my co-teacher and I changed our focus on the fly in a moment of teaching epiphany. The kids (as they often do) let us know the best way to keep their attention.

Lesson Structure:

We began by running through what coding was, and how we can communicate with robots through a series of steps called an algorithm. We ran a couple simple movement algorithms for the kids and the excitement level was immediately through the roof. The room was alive with collective “oooohs” and “awwwwws” as the robot moved, flashed its lights, and made sounds. When we sent them to work on their initial estimations, the room became a flurry of focused activity. 

We had outlawed the explicit measurement of the course, but did allow the kids to use measurement tools as referents. They also had a collection of personal referents for certain lengths³. One of the more popular methods was to pace along the course using the length of their stride or length of their foot as a rough measurement tool. A few other students used their thumb and index finger as a 90 degree angle and then squeezed them together to approximate the angles. 

One interesting fallout from estimating the path of the robot was that students needed to estimate the degree that the robot needed to turn as if they were driving the robot. Several groups ended up estimating the incorrect angle, and this was very evident when they provided their code. However, after analysis with the class, the class decided that they estimated well, but they were just looking at the wrong angle. Relationships between supplementary angles and even reflex angles (a term they were familiar with) emerged. On a few occasions, students listed both an angle and its supplement as possibilities. 

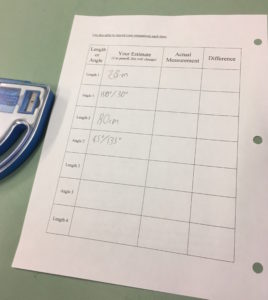
We gave each group a 2-minute warning, and then asked if there was a group that wanted to submit their coded estimations first ⁴. It was here when we realized that we would not need to have them average. No group wanted to volunteer, because they were all looking for more information. They wanted to see what the other’s estimations yielded before they provided their answers. This meant that students were not just “guessing,” as estimation is often misconstrued to be. They were using, evaluating, and refining their intuition for the size of lengths and angles. Much like reading a putt in golf, the class saw going later as an advantage. It was at this moment when my co-teacher and I looked at each other and simultaneously said that we didn’t need averaging; we knew we had them hooked. We got a volunteer group to start and while their course was being run, there was total silence and attentiveness until a “mistake” was made. Then the groups re-convened in hushed conversation to alter their predictions before it was their turn. 

After each group had two opportunities to refine their estimates (based on the ever-growing collection of information), my co-teacher and I took a stab at it. I would say that we finished second, but the students might object to that. 

Conclusion:

There was no denying the obvious energy the robot brought to the lesson. Even as the students filed in, you could hear remarks like, this is going to be interesting and woah, cool. There were moments when their faces looked like the students in those stock photos where everyone loves math and the teacher is their superhero. Students wanted to name their robots, they cheered for them, we even coined the phrase, “Don’t be a Gerald” after one robot (nicknamed Gerald) was coded with an obtuse angle instead of an acute supplement. 

What I am most impressed with is the way that the mathematics remained the focus of the day. When it got loud, the room was filled with conversations about angles, lengths, referents, and data. The interaction with the InO-Bot fueled meaningful interaction with mathematical ideas. I believe that this should remain the focus of this technology in the classroom. Now the challenge is to expand the outcomes that InO-Bot can support. 

 NatBanting

1. Canadian Classroom is a Canadian distributor of a wide variety of STEM products
2. I encourage everyone to go play with Scratch. The capabilities of robots like the InO-Bot only add possibility and engagement.
3. The use of referents is an outcome in our curriculum.
4. Because each group was trying to follow a set path, the string of commands were identical. This was by design because this was an introductory activity.