A colleague and I have often bemoaned our attempts to teach the concept of scale factor in higher dimensions. A topic that has such beautiful and elegant patterns and symmetries between the scale factors consistently seems to sail directly past the experience of our students. I have tried enacting several tasks with the students including some favourites from the #MTBoS (Mathalicious 1600 Pennsylvania and Giant Gummy Bear). Each time, the thinking during the task seems to dissipate when new problems are offered. It just seems like students have a hard time trusting the immense rate that surface area and volume can grow (or shrink). In the past, I had used digital images of cubes growing after having their dimensions scaled by 2, 3, 4… etc.; students seemed to grasp the pattern yet under-appreciate the girth of 8, 27, 64… etc. times as many cubes.
For this reason, I went looking for a way to concretely demonstrate these phenomena. I wanted them to feel the weight of increasing volume.
I settled on a simple construction activity, one that I’m sure has been enacted in several mathematics classrooms. This post isn’t as much about a great idea as it is about a reminder that simple designs can sponsor elegant mathematical action.
I randomly grouped them into 3s, and assigned each group a total number of linking cubes they were permitted to use. These values ranged from 6 to 9 total cubes. Each group was instructed to combine the cubes to make a shape of their choosing. Now, anyone who has taught middle school needs to know that the irresistible tendency for students to build guns and swords does not dissipate by the 10th and 11th grade. Many, but not all, groups created designs that laid flat on the table. That is, they had a “width” of 1 block. At first I was hesitant about allowing this characteristic to crosscut through each group, but it turned out to be very valuable later on. (see The 2D Builders).
When all the shapes were complete, we defined each dimension of a cube as 1 centimetre. This made “calculating” the dimensions, surface area, and volumes of the arrangements a matter of counting. 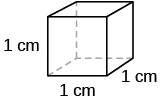
The groups were each asked to determine the surface area and volume of their linking cube arrangements. They kept these values on their group workspace, and then I gave the prompt:
The 2D Builders.
 |
| Group builds an enlarged cross by layering two separate cross designs. |
These groups all built shapes that were one cube “thick”. They constructed their new, enlarged arrangement by doubling the length and width of the shape. Several groups left their work here, and needed to be prompted to double the “thickness” of the shape as well. Generally, I took a subtle approach to this intervention. I would ask them to prove that they had doubled every dimension, and mention, in passing, that the heights still matched–total passive-aggressive teaching move.
The 1-is-8 Builders.
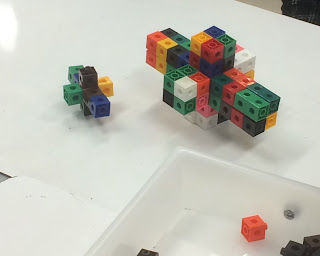 |
| Group builds an enlarged shape by re-enacting the initial construction with larger constituent cubes. |
This strategy seemed to emerge from groups with more complicated arrangements. In order to double every dimension, they dissected their original shape into the constituent cubes and doubled each of their dimensions. It wasn’t long until the news spread around the room that one cube just becomes eight cubes (a fact that led perfectly into the discussion of volume scale factor). The new, enlarged shapes were then built in an identical fashion as the originals, by constructing new, larger cubes in groups of eight, and then attaching them together.
The Partial Doublers.
 |
| A “camel” shape is partially doubled. |
 |
| A “stairs” shape is partially doubled. |
The Dimension Doublers.
 |
| Group builds new, enlarged shape by doubling every edge of the original shape. |
These groups did not dissect their original shape, but counted (and often recorded) each dimension. Then they simply doubled each number and re-constructed a shape based on the new blueprint with little reference to the original shape. This abstraction resulted in accurate enlargements.
When I envisioned the activity, I thought I would spend most of the time focusing on the results of the doubling, but the conversation regarding the various strategies was too irresistible to ignore. After I had groups describe how they went about completing the task, I asked them all to calculate the surface area and volume of the new, enlarged shape. We created a table at the front of the room to record the results of the constructions.
I then collected the results from the groups. As we went along, each response was recorded without judgement from me. There were times when the emerging pattern fell through and students alerted me to this fact. I would ask for clarification, place a “?” next to the entries in question, and ask the groups to double check their calculations. By the time the last few groups were offering their values, they had become completely predictable.
Opportunity knocks, so you open the door. We spent some time predicting what would happen to the surface area and volume if we tripled each dimension. These were exactly the types of conversations I had hoped to trigger. When I do this again, I think I will have some type of sticker that I will ask groups to use to “count” the surface area. I feel like we spent a lot of time experiencing how much greater the volume grows, but glossed over the growth of the surface area. Having them place a sticker on each face might begin to build an appreciation for the growing surface area as well.
To reiterate, this idea is not new, nor mine. I would credit it to two things. First, the incessant joy Alex Overwijk gets from playing with linking cubes. (I am often jealous of the uses he finds for them). Second, the recognition that great thinking can emerge from modest tasks and problems, and it is the ability to remain sensitive for those opportunities that can create powerful learning experiences from meager beginnings.
NatBanting

