Discussion is one of the organic ways through which human interaction occurs, but not all discussion is created equal in the math classroom. The tone of discussion relies on the mode of listening (Davis, 1996). Most classroom talk focuses on an evaluative mode of listening. Students are expected to share, compare, and contrast solutions to problems.
I do think that justification of their solutions gets at some important points regarding mathematical reasoning, but would like to move the discussion to center around that exact feature–the reasoning.
Rather than piecing together the pieces of isolated reasoning (which I still think has value), I want to see a collective reasoning emerge through the discussion. Students don’t “think-pair-share” their solutions; students bring their conceptualizations and reason to a collective understanding. There is something about the power of this collectivity that makes the learning unique. (And I am insanely interested in how it differs, why it differs, and if it is viable in a classroom).
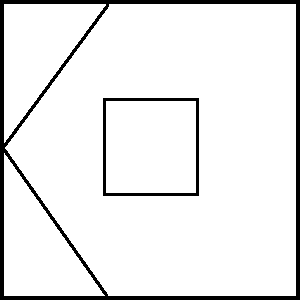
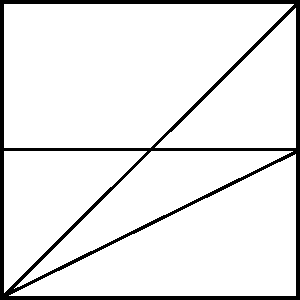
To try and harness this type of reasoning, I created (with my students) a series of “Fraction Squares” inspired by a keynote given by Ilana Horn and SUM2015. They all involve a dissection of a square using straight lines.
I project a Fraction Square, shade a section, and ask, “What fraction of the square is shaded?“
I moderate the discussion and entertain all solutions. It isn’t long until the discussion no longer runs through me. The students turn, pull out paper, run to the board, and justify their thinking.
As they talk about slicing the sections into pieces, I do my best in interject precise vocabulary. For instance, a student might say, “A half of a half is a quarter”, and I may probe this to elicit which operation they are really talking about. I don’t push the standard algorithm of multiplying fractions, but write number sentences beside their quotations.
This way, the vocabulary and notation is slowly imbibed into their collective action. Students start to talk about the four operations (instances of division by fractions are rare), and the number sentences act as a bridge to conceptualize the standard fraction algorithms. It provides an active visualization of processes like creating a common denominator. The picture is not presented and explained; the picture is presented and then acted out through collective discussion. In a sense, it becomes personal.
Some groups may focus on certain lines of argument, and others find them completely disinteresting. It is the job of the teacher to remain fluid, keep end goals in mind, and network the collective.
Some other prompts to use:
Above are a few more examples of fraction squares my students created this year. After a few fraction talks, have your students do the same and then exchange them. These seem to introduce enough perplexity to facilitate a collective discussion where students think out loud to arrive at a strong conceptualization of part-whole relationships.
NatBanting
Davis, B. (1996) Teaching mathematics: Toward a sound alternative. New York, NY: Garland.


5 replies on “Fraction Talks”
Great ideas. I use to use an overhead with coloured opaque tiles that were arranged in a square. Not as easy to make different forms. This offers so many different options. The great thing is the ability to share with other students and share their thinking. Collaborative groups for sharing their ideas and thoughts is a great way to help students work through their thinking – having them share helps all students especially with fractions. Thanks for sharing your work and what you are doing!
Hello! This post was recommended for MTBoS 2015: a collection of people's favorite blog posts of the year. We would like to publish an edited volume of the posts and use the money raised toward a scholarship for TMC. Please let us know by responding via email to tina.cardone1@gmail.com whether or not you grant us permission to include your post. Thank you, Tina and Lani.
Awesome ideas! I love the individual and collaborative aspects.
Quel fabuleux travail! La collaboration est un excellent moyen pour partager les idées et permet de parfaire les stratégies de résolution de problèmes.
This is great, we do number talks, but to have fraction talks is a perfect way to help understand fractions!