Occasionally, I give a task to my students before I have done it myself. Sometimes it is because the solution is fairly straightforward and I can see multiple ways to arriving at it without actually doing it. Other times it is because I want to have no impact on my students’ thought pathways. The practice also makes class time more exciting as students reason through methods that I would not have though of–I am trying to move from a monotonous state of lesson planning to a more exciting one of lesson participation.
About two weeks ago, I was preparing a unit on surface area and volume for a new course in our province. I sent a tweet out asking for any “favourite problems” that people may have on the subject, and got multiple responses. Three or four of them have made their way (in various states of modification) in to my unit plans in the form of projects, problems, and tasks, but one in particular stuck with me. Although it would have been great to first “do” the problem alongside my students, curiosity got the best of me and I began to puzzle it out. The question, courtesy of Andrew Kelly (@bewdyrooster) is as follows:
First off, I love the way the problem was posed to me. He didn’t include an elongated set of instructions which defined every aspect of the problem. I was left wondering various things:
- We know the holes are square, what about the solid?
- Would this work for solids with more faces than a cube?
- Would the solids have to have a even number of faces?
- Are the “punch-outs” centered?
- Are they a certain ratio of the side area?
- What is the original side length?
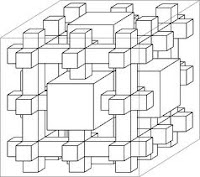
Good numeracy tasks are presented with sufficient vagueness to entice curiosity. This did the trick. I looked up “Menger Sponge” on Google, and began to define the characteristics of the problem.
- The solid is indeed a cube
- The punch-outs are to be 1/3 of the existing dimensions, for a total of 1/9 the area
- The punch-outs are centered
I set out to answer the original question, but like all good problems, I discovered many more questions, problems, viewpoints, and applications as I went. I will discuss the applications to a high school curriculum later on. I began my thinking like this:
- The cube has six sides, so the “punch-outs” would only have to be done 3 times (all the way through).
- If I begin with volume, the removed pieces will consist of 3 rectangular prisms.
- There will be an overlap in the center where all three meet; I will have to subtract that area twice.
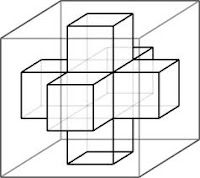
Seemed pretty water tight, so I went to work. I was envisioning the first two sets of cutting to look like this:
My vision got complicated quickly. I had to develop a formula for the total number of prisms to be cut out. If that wasn’t complex enough, I had to decide how many times the cutouts overlapped and subtract the volume not being removed. Do the corner pieces overlap more times than the side pieces? How do you classify a corner and a side as “n” increases? The entire process was quickly slipping out of the scope of my class until my wife came in to check on my progress.
I explained my thinking, and she had a glorious insight. Thinking of the “waste” as rectangular prisms was over complicating things; because the cut-outs had identical dimensions and were always cut out on the same plane, their overlap formed cubes. We (notice the pronoun change) could then view the entire solid as a sum of cubes made up out of the smallest “punch-out” dimension.
What was better, we could actually take the first, solid cube and build the next step out of 20 cubes. Because a 3×3 cube should be made up of 27 smaller ones, it was plain to see that 7 had been punched out. The task became much simpler, and suddenly accessible to a wide variety of high school mathematics. We began to view the cubes as sums of smaller cubes:
The transition moved our thought pattern from calculating volumes of rectangular prisms to counting cubes of a uniform volume.
A change in perspective led to powerful learning. My active participation in the “lesson” (bolstered by a different viewpoint) ended up unlocking potential for the problem.
The original question asked for a pattern in the volume and surface area of the cube. As the “n” increases the volume seems to approach zero while the surface area approaches infinity. As I continued building the models in Google SketchUp, many other curricular connections emerged:
-
Linear functions.
-
What if we “built” a Menger cube, instead of poked holes in it?
-
If n=1 is composed of 20 n=0 cubes, and n=2 is composed of 20 n=1 cubes then you could set up a function to calculate the volume of the growing cube.
-
-
Infinite Sequences and Series
-
Again, with the building of the cube.
-
Could calculate the total number of cubes in a “n=x” cube by finding the “x-th” term in the sequence with a first term of 1, and a common ration of 20. (because it takes 20 cubes to build the next Menger model).
-
-
Basic Exponents
-
Students could calculate the volume of the cube by calculating the missing pieces.
-
It would give a visual representation of a cube combined with some intrigue.
-
How many cubes should the picture have? How many does it actually have? Can you find the pattern of construction?
-
-
Surface Area and Volume
-
Its original intention
-
Track the trends of the Surface Area in the lower iterations and Volume in the higher iterations
-
As you can see, the problems carries elementary and sophisticated extensions. I loved the problem in the beginning for its intrigue, but it wasn’t until I participated in the lesson that I learned its true versatility. Facilitating an effective (and enjoyable) math class hinges on the teacher’s ability to see potential in problems. In some cases, that vision is possible without ever doing the problem. In other cases, the most powerful planning comes through authentic participation.
NatBanting
6 replies on “Lesson Planning; Lesson Participating”
Beautiful exploration. Whether to "plan" or "participate" depends an awful lot on what one hopes to teach, right?
If you want to teach problem posing, problem solving and the like, then it makes sense to participate. Students would benefit from seeing a sophisticated mathematical thinker struggle through these things.
But if you want to teach a particular piece of content, or a particular strategy or set of strategies, then the folks at University of Pittsburgh have been developing pretty strong evidence that you do need to work the problem first, and you do need to know how students will approach the problem.
But those are two different sets of purposes. I'm not sure the research has anything to say about teaching generalized problem solving.
Wow. Sorry I mentioned it. Great work. I did pretty much the same analysis. As a practical way in, you can make cubes from business cards – google business card menger sponge, or go here http://theiff.org/oexhibits/paper06.html or go here http://fyels.com.au/467 to see a worksheet I put together one time. Feel free to alter/reuse if you like. I have a (what I would call) n=2 sponge on my desk at school made my a couple of keen students. And I like the way that your wife being involved in the argument/discussion – maths as a social activity – woot.
Good luck. I have an aim in my maths class this year (with 14 year olds) to get them to build all the platonic solids – each in a different way. Because it's fun, interesting, and they'll work together.
@christopherdanielson When I said I neglect to "do" the problems sometimes it is because their simplicity coupled with my math background allows me to "do" them very easily. I guess you could call it an implicit solution rather than an explicit one. I know what the problem will present to my students. There are problems, however, that present novel solutions as I take part. Those are the ones I value participation in becuase what I thought was being learned may lead into different and (in some cases) more valuable learning. Thanks for reading.
@bewdyrooster haha… I am very glad you gave me the suggestion. I am going to use this problem with my surface are and volume unit in a PBL focused class. It will be a good problem for the students. I also was looking for problems with exponents because my Ss just did particularily poor on that section. This may be a cornerstone of that remodeling as well. Thanks again (for reading and suggesting)
Nat, what a great problem, though I have to admit that the infinite series lost me along the way.
I think the first cube is interesting enough to use with elementary students – would you agree? So much elementary "problem solving" is based around routines recently taught; I'm always looking for more interesting examples like this.
Nat: I guess you could call it an implicit solution rather than an explicit one. I know what the problem will present to my students.
Yeah, about that…I admire the swagger (and possess a good deal of it myself), but I also know I'm a better teacher when I've done the hard work of committing to the student strategies I expect. I wrote about that last year. I'd be curious to know your thoughts (n.b. productive discussion occurs in the comments on that post.)