[Update Nov 4th, 2021: Since this initial post, I have intentionally backgrounded the term “#FreeScalene” because I am now at a place where I feel that facetiously couching a classroom activity in this language treats the work of important social movements with too little respect. I leave this post here (complete with this addendum) because this blog is a place to archive my professional trajectory, and I feel this update is an important piece of that growth.
If you want to read my thoughts on the merits of debating geometric definitions (especially triangles), portions of this post are expanded upon here.]
[Original Post: Published March 2020]
This past weekend I was invited to Toronto to give the 2019 Margaret Sinclair Memorial Award Lecture at the Fields Math Ed. Forum at the Fields Institute for Research in Mathematical Sciences. While the layers of the organizational hierarchy can be a mouthful, the bottom line is that I was given the great honour of presenting my thoughts on the teaching and learning of mathematics–as they are formulated at this time of writing. I broke the day into three distinct sections: The recipient’s lecture, a poetic provocation about hotdogs and mathematics education, and a gallery walk composed of some of my favourite invitations from my career to date.
(Link to the video archive of the invited lecture.)
As has become my custom (inspired by the gentle chiding from Mary Bourassa), I undertake these speaking opportunities in a signature garment that has become affectionately known as a “conference hoodie”. Aside from being outrageously comfortable, this particular conference hoodie addressed what I consider to be a well-overdue mathematical misstep. In 2016, a class of ninth graders and I coined the term #FreeScalene while exploring the inconsistent classification of the much-maligned scalene triangle.1 Over the years, I have used this tagline to sponsor a geometric campaign (of sorts) in defence of the positive qualities of the scalene triangle (in particular) and awareness of the important role of mathematical definitions (more generally). This has resulted in heated arguments, social media posts, journal articles (Excerpt here; full-text here–if you can get behind a paywall), a custom T-shirt gifted to me from supportive students, and rich mathematical sense-making. I decided that the Fields Institute was the perfect stage to make my case for #FreeScalene.
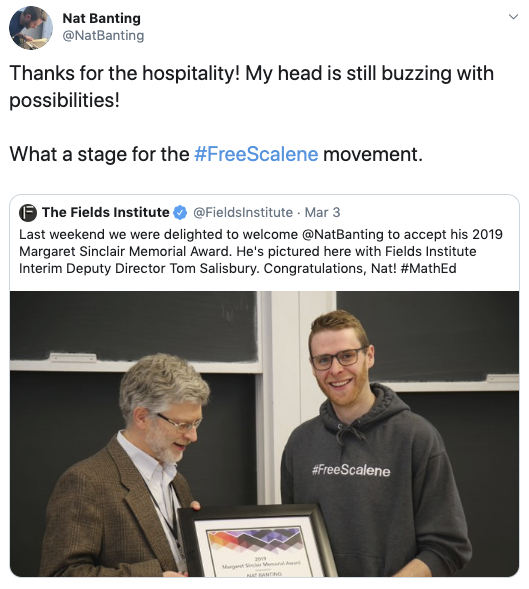
Now, I didn’t bother introduce any of this to the attendees, but it wasn’t long before questions of the origin and meaning of “#FreeScalene” emerged. Here, I make a brief case in support of the legitimacy of #FreeScalene both mathematically and pedagogically.
Mathematically:
Mathematical classifications stem from mathematical definitions. Therefore, it is crucial that we explore the issue at its root: the definition of “scalene”. If we restrict consideration to triangles and quadrilaterals (due to their familiarity in the grade school outcomes and standards), it quickly becomes apparent that the scalene triangle is the only shape in this set that is defined based on what is does not have, while all others are defined based on what they do have. The definer, by adopting these definitions, is already implying the poor scalene triangle is wanting. While parallelograms (for example) enjoy being defined (and classified) based on things they boast (two pairs of opposite, parallel sides), the scalene triangle is subjugated to wallowing in its deficiencies–that is has no congruent sides. Seems unfair.
And it doesn’t stop there. Conventionally, all quadrilaterals and triangles share a hierarchical classification system that nests, for example, more specific shapes (like squares) as sub-categories of more generic shapes (like rectangles). Because a square still suffices all requirements of “rectangleness,” it does not forfeit the classification as “rectangle” to also gain a classification of “square”. The same goes for rhombi retaining their classifications as trapezoids and parallelograms. This convention extends to triangles–well, for a privileged subset of triangles. Conventionally, an equilateral triangle is defined as having three congruent sides, which satisfies the isosceles requirement of having two congruent sides–having three congruent is having two congruent. However, the scalene triangle is blatantly excluded from the hierarchy because it is defined exclusively as having no congruent sides.
Perhaps you claim that’s just the way things are. It’s a big, bad 2D plane out there, and there will be casualties in any system. However, I am claiming the term “scalene” is completely superfluous. Please indulge my assertion by naming a triangle more generic than the scalene triangle. That is, what requires the descriptor “scalene”? Surely there must be some distinction between “triangle” and “scalene triangle” to necessitate this term!?!
If you take the conventional hierarchical classification to its generic limit with quadrilaterals, you arrive at the most generic quadrilateral possible: A shape with four straight sides. We call this shape a “quadrilateral”–not a “scalene quadrilateral”. If we undertake the same exercise with triangles, the scalene triangle is the most generic shape that still suffices the requirements to be a triangle: It has three straight sides. So why the pejorative moniker of “scalene”? It is unnecessary and mean-spirited.
I give the last word to geometer Dr. Walter Whitely who brought it to my attention that, in terms of geometric transformations, all triangles are equal.
Pedagogically:
This section need not be as long or arduous as the previous. I have spread my pedagogical convictions across the pages of this blog, and expanded upon my theoretical assertion in “teaching as triggering” during the course of the recipient lecture. The goal of #FreeScalene is to provide disruption, and the role of the teacher is to dwell in the sponsored uncertainty rather than to define it away. (A lesson I learned, and continue to learn, from Christopher Danielson). By playing with possibilities, we gain an appreciation for the characteristics of, and relationships between, elementary geometric shapes; we also gain an appreciation for the role definitions play in mathematical sense-making. Above all, the satire of #FreeScalene is designed to provoke students to tinker with possibility, invite them to make sense the fallout, and remind us all that mathematics is a participatory venture.
NatBanting