For the first time in a decade, I am not reconvening with a high school staff to begin preparations for the school year. (I’m preparing to work with pre-service teachers on a university campus). It feels weird–very weird. It is a day that I look forward to because optimism is a constant across the building. Staff feels fresh, materials are crisp, and possibilities are endless. It sadly belies what’s to come.
Bummer, right?
The marathon of a school year is taxing. As math teachers, we are asked to design an experience that maintains a perpetual novelty between a set of students with a cacophony of histories and a set of standards that feel inherently phobic to the variability of humanness. It is not uncommon (at least for me) to come up for air in a few months only to feel like the classroom has lost all its lustre. Sure, they are complying, but the classroom lacks the buzz of the first few days. In these moments it’s simple to resign yourself to the impression that the buzz of the first few days is unique to the first few days. This post is about refusing to participate in that resignation, and I think this time of year is the best time to receive that message.
Last year I had a group that would. not. act. They just wouldn’t. I tried every move in every conceivable pedagogical playbook to increase the engagement in the classroom, but each was met the same way: indifference. They were executing mathematics, but were not acting in mathematical ways; they were meeting the content goals, but not the course goals. You name it; I tried it.
On this particular day, we were in random groups working on netting composite solids. I printed off several diagrams and posted them around the room. Groups were instructed to dissect the composite solids into nets, and use those nets to calculate surface area. We had calculated areas before, so my focus was on the spacial reasoning necessary to work with three-dimensional shapes in a two-dimensional capacity. I was exhausted. I didn’t expect much innovative thought to come from the activity partially because I came to expect a lack of innovative activity on the whole. The project of teaching mathematics had won. I had nothing.
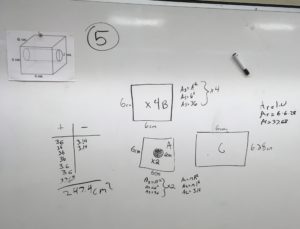
I circulated and questioned groups on their nets and calculations. I got to station #5, and was met with a student’s comment:
“This is dirty”
[He gestured to the rectangle they had labeled “C”]
“What kind of cube has seven sides?”
I responded in the best way I could in the moment, “I didn’t ask about sides. I asked about surfaces.” And then it hit me. By accident, I had provided an occasion of intrigue. Every cube these students had ever seen had resulted in the exact. same. nets. On top of that, they were only every asked to think in one direction: from 3D to 2D.
Rejuvenated with this new possibility, I asked them to turn over their diagram and wait. I blitzed around the room asking all the groups to do the same. Then I grabbed everyone’s attention and asked them to do something unconventional: erase everything but keep their nets and dimensions intact. In that moment, it felt like the first day of school.

I had each group rotate one station clockwise and complete the following task:
Re-construct the solid that produced these nets. When complete, use the nets to calculate the surface area of the solid
The room came alive; I came alive. I felt like a teacher again–not just a teller. Groups started to interact, hypothesize, and debate. Some used the dimensions to “match” sides together. Others began with difficult shapes (like triangles and circles) and used rectangles to complete the designs. Some began by counting the rectangles, and deciding what types of shapes would contain that many rectangular sides. I worked to extend the action:
“Build be a solid that would have a very similar set of nets. Similar enough that some may confuse the two”
“Add one piece to the diagram that actually reduces the total surface area”
Conversations revolved around these strategies and not around a play-by-play list of steps that they were taking, and we ended class by ranking the solids from simplest to most difficult to re-construct. I almost ran around the room for a solid 40 minutes, but did not feel exhausted in the least. I felt the exact opposite: I felt like the first day of classes.
Why this post at this time? First, I think the task of building composite shapes from 2D nets is a profitable one for occasioning student spatial reasoning. Second, I think it holds important messages as we begin another school year:
- Listen to your students. Attend to what they find curious. Not all possibility is pre-destined, but many come from the nooks and crannies of interactions. Run with them; that’s the spirit ensconced in the start of the year activities. Don’t lose it in November.
- Look for the little variabilities that pique your learners’ interest. Take information away, switch the direction of activity, or have them build to specifications. Lots of possibility comes from acting in novel ways with familiar mathematical objects.
- Keep pushing; keep working at it. Relentlessly pursue the thinking that matters.
NatBanting