I recently finished up a unit on sequences and series with my grade 11 pre-calculus students. The unit is somewhat of an enigma because it contains relatively simple ideas bogged down in complex notation. This coupled with the overlapping definitions makes for a fortnight of rather rigorous cognitive exercise.
The unit was supported through group tasks as the topics moved along. Arithmetic sequences and series were linked to linear functions through the toothpick problem. Students were asked to arrange toothpicks into boxes and record how many toothpicks it took to make ‘x’ number of boxes. Their results were extrapolated and tied to variables from the linear functions notation. From there, I introduced the new terms of “common difference” and “term one” instead of slope and y-intercept. The arithmetic portion usually goes smoother than its geometric cousin for two reasons:
1) The members of the sequence are equally spaced in an arithmetic sequence
2) The arithmetic situation avoids large and ugly fractions
I introduced the concept of geometric sequences with a video clip from “Pay it Forward”. The clip, found here, used a familiar situation to show the new relationship between terms. Students commented on how quickly the results grew in this new case. One student asked if all the answers were going to be so huge. Before I could respond, another student retorted that very large numbers are better than very small ones. With an inward smile, I seized my chance to begin the shaded square.
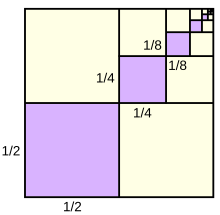
I handed out a simple sheet to every student. On it were 2 squares–one on each side–and room for a few calculations below. I put three steps on the board, modeled the process for one iteration, and stepped back to let them answer the question.
1) Cut the unshaded area in half.
2) Shade in one side of your bisection.
3) Repeat.
How much area is shaded with each iteration?
What pattern do you notice between each successive number?
From here, I had to work quickly. Students’ pages are only large enough to give 6-7 cuts of the square before they run out of feasible space. I circulate to make sure that the cuts are being made as logically as possible.
The space for calculations is used initially to find simple common denominators, but I found that most students pick up on the pattern quickly. Students begin to list the terms in the familiar sequence notation:
(1/2), (1/4), (1/8), (1/16), (1/32), (1/64), (1/128)…
The pattern then needs to be translated from a “division by 2” into a “multiplication by 1/2”. Other problems are presented to work on geometric sequences, and we return to the square a few days later with the topic of series. The question changes slightly:
From:
“What fraction of the square is newly shaded with each iteration?”
To:
“What total fraction of the square is shaded after each iteration?”
We check the sums after a few iterations, but the students soon grow sick of calculating common denominators. The true value of the shaded square problem comes when I introduce infinite geometric series; the concrete nature of the problem brings some sanity to a counter-intuitive situation:
You can add a positive number forever, and never get past a certain point.
I introduce the words “limit” and “convergent” to the dialogue. Will the shading ever stop? Will you ever be able to shade outside the square? Such questions are trivialized to begin with. The shading won’t end unless you stop, and of course you can’t shade outside the square if you only cut remaining area. The answer, almost logically, converges to a sum of 1.
The problem opens a window of understanding into infinite possibilities. Change the problem; allow students to carry out different ratios and estimate their sums. The formula is always there to check answers. If you give the formula without explanation, it becomes a crutch–not a tool. Try dividing the remaining area into 4 pieces and shading one. Carry out this method to get an image like this:
Credit: http://en.wikipedia.org/wiki/Geometric_series
My students immediately noticed that the sum must be more than 1/4 and less than 1/2 based on solid and empty quadrants. What will your students notice? What if the cuts with the 1/2 variation were made vertex to vertex creating identical triangles? I had several students do this. This involves more complex algebraic manipulation.
It was shocking to see my students’ nonchalant response to the questions of convergence. The situation provides an excellent concrete base for a difficult topic. It also provides a loose enough environment to foster group discussion and peer collaboration. The idea of infinity is intriguing, but difficult to grasp. The shaded square is an excellent tool to rationalize the fact that we can add forever and never break (or reach) a certain point.
NatBanting