I don’t mind the staffroom. I share a prep period with my math department head, and we often engage in meaningful conversation about the ongoing struggle of curriculum renewal. It is an unbelievable support to have a leader who is so willing to learn about what the reform approach has to offer. Teachers do not spend near enough time learning–which is an ironic shame.
One morning, I walked into the staffroom and he greeted me with a question:
“What’s new in math education today?”
I didn’t pretend to be on the cutting edge of everything math education, but was working through a problem that I read before bed the night before. It came from James Tanton’s book Solve This: Math Activities for Students and Clubs. The question itself was very subtle:
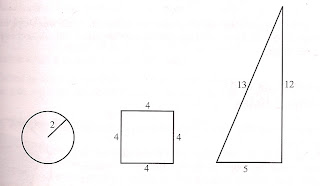 |
||
| Tanton, James. Solve This: Math Activities for Students and Clubs. p. 5 |
Tanton simply asks, “The figures share a curious property. What is it?”
It only takes a short while to realize that the area is equal to the perimeter in these three figures. Most traditional mathematical training is focused on looking at the numbers and plugging them into some kind of formula. Area and perimeter are the first two that spring to mind. My interest in the problem was a little deeper, and I shared that with my questioner.
I explained a list of questions that I had documented on my BlackBerry the night before:
- Does this property exist for shapes with more that 4 sides?
- For how many triangles must this property be true?
- Can I find any more?
- Can I create a foolproof system to devise triangles with this property?
- What must the side length of a pentagon with this property be?
- Must the polygons be regular to have this property?
- Do these figures share any other curious properties?
He immediately pulled out a pen and grabbed for a errant napkin on the nearby table and we started doing mathematics. His background in computer programming and my background in number theory allowed us to find higher order similar polygons with the property. The contagious nature of mathematics shone through. An English teacher, also with a background in mathematics, came over and inquired about the problem. The three of use poured over the project until the break ended. The experience taught me two things:
- Teachers are curious people deep, deep down.
- Math teachers do not spend enough time engaging in mathematical activities outside of their students’ work.
Later on in the day I was contacted by another math teacher–a good friend–about the problem. In the middle of class I received an instant message from him saying that he heard the problem and was wondering if his solution was correct. We sent a series of messages back and fourth about his dilemma.
After school, I was discussing the problem with him again and two other teachers walked in and gave their input. Something motivated these teachers, from multiple disciplines, to do the problem. I think it was a potent mix of availability, pride, and anxiety. Most of these teachers had a bad experience with math in school; some were solving their first interest based math problem ever. It served as some kind of vindication for them.
The whole experience made me wonder; how much of professional development is spent modeling reform techniques? More often than not, teachers are herded into rooms to hear an expert preach about assessment or differentiated this-and-that. Why don’t math teachers ever get opportunities to feel what real mathematics is like?
I think if we tried it, we may just discover who is cut out to be a math teacher. Learning is infectious; if students see teachers engaging in problems with each other, they will be more willing to engage in them personally. Teachers would be more open to change if they experienced the change themselves.
NatBanting
Tanton’s book comes recommended not only as a resource for “students and clubs” but also for teachers. It can be purchased online.