**Update November 2020. Jamie Mitchell–a fantastic teacher from Ontario, Canada–sent me this google doc that his student prepared to justify her solution. After you wrestle with the prompt for a while, take a second to read this brilliant response!
Most probability resources contain a familiar type of question: the two-dice probability distribution problem.
Often times, it is accompanied with questions concerning the sums of the faces that appear on each dice.
For example:
I think the obsession with this specific subdomain of probability questions stems from the elegant way in which a table of outcomes (pictured below) leads to a counting of favourable and total events.
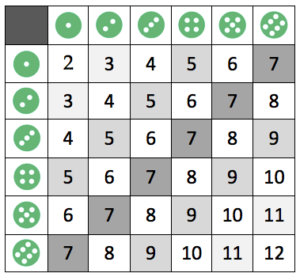 |
| The sums of two dice neatly organized into a table. |
Shifting the problem ever so slightly offers a new sub-domain of question concerning the product of the two dice. A typical problem might look like:
c) the product is greater than 15?
Note the small shift necessary to surround the problem with the same structure of a table of outcomes (pictured below). I am assuming that most teachers of mathematics could construct numerous additional sub-questions of the same variety. The question grows in size, but remains one that requires simple counting.
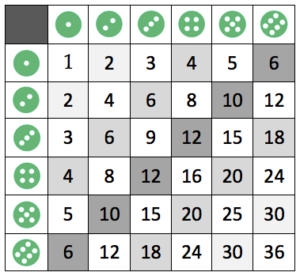 |
| The products of two dice neatly organized into a table. |
I believe these types of questions are a direct result of math teaching’s infatuation with tidiness, especially within the content domain of probability. This is unfortunate, because probability offers accessible forays into imagination and allows intuition to play the dual, contradictory role of guiding light and devil’s advocate. In other words, posing an elegant probability problem leaves the solver balancing their wonder (driven by the question, “what if?”) with their rationality (driven by the assertion of, “that can’t be!”)
In an effort to make this domain of two-dice probability distribution problems more interesting, I flipped* them.
[Sidenote Rant:
It should be noted that opening up a problem to divergent and emergent action does not de-value the elegant organizations afforded to mathematics. Many think that rich, open tasks are just a rejection of neat and orderly work. However, open tasks signal a rejection of the notion that interaction with a problem should be neat and orderly, and, by extension, that learning mathematics is the process of achieving lockstep with an ideal way of acting. The learning of mathematics is a holistic, messy, and convoluted experience filled with triumphs, dead ends, and ways of representing action. In order to harness these movements, the problems need to allow space for them. The structure of the table of outcomes may well emerge as useful to students working on this problem. In fact, as you will see below, it was eventually encouraged, but not legislated.
End Rant.]
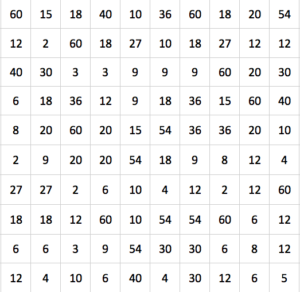
As a frame of reference for the students, I offer them the following image of 100 products from two standard dice.
- Are both dice identical?
- Can a number appear on a die more than once?
- How many faces are on each die?
- Can the faces have fractions or decimals?
- etc.
In this case, I refine my parameters to two dice, each with six sides. The dice do not have to be identical, and all faces from both dice feature whole numbers. A number can appear more than once on a single die, and that will be reflected in how many times certain products are created.
Part way through their action with the problem, I provide them with two handouts. This helps them structure their work (if necessary), and provides them an artefact to hand in to me when the time comes.
The first is a sheet with a completed table of products from two normal dice (similar to the first image in this post) and the corresponding nets of the dice that would create the distribution. (download .pdf here). The second is an identical sheet with the table and dice nets left blank for them to work with when creating the dice that resulted in this new distribution. (download .pdf here).
I give each group a single copy of each handout (to eventually hand in) and have them do the majority of their work on a shared whiteboard space. I find the communal (and non-permanent) workspace to encourage a greater density of neighbour interactions.
Anticipated student action:
I’ve chosen to organize anticipations of student action around possible questions that 1) groups may pose during the course of action or 2) teachers may pose to trigger student action or perturb student reasoning.
(1) Will all possible combinations of rolls occur in the 100 trials?
This question gets at the very heart of probability. I guess, in theory, the answer is: No, not every possible pairing must have been rolled in the 100 trials. But there are three caveats to this: First, every product must be possible. That means that all products must have at least one pair of factors that exist on opposite dice. Second, how many products are there? If there are less than 36, that doesn’t mean that some did not occur. It could mean that some have multiple factor pairings that produce them. Third, each outcome has a 1 in 36 chance in happening. Even if each product were unique, there would still be a good chance that each occurred in 100 rolls.
(2) Does where you place the factors make any difference?
We assumed the dice were fair so where you place the numbers on a single die will not matter. However, switching numbers between dice will change the possible outcomes. Keep in mind that each product needs to have one factor on each die.
(3) How often will certain outcomes occur?
My guess is students will set up some type of table of results and compare the experimental results with a dynamic theoretical probability as they build their dice. They will feel comfortable when their theoretical calculations closely match the experimental results. If they set up a system where “6” should be rolled 5 times in 36, but only appears 7 times in the 100 trials, are they wrong? What is the margin for error? What if theoretically rare outcomes actually appear more often than theoretically common ones in the trial? Should we be switching numbers, or assuming that the trial resulted in a deviance from expectation?
I think the beauty of the problem is in this question. Arguments are rooted in theoretical mathematics (which are most likely emphasized in the curricular outcomes), yet guided by experimental probability. In the middle space between the two exists mathematical intuition.
(4) What do prime numbers tell us?
Well, a prime number has two factors, so we know those two factors must exist on opposite dice. Also, one of those factors needs to be a “1”. The case of “1” is interesting. How can we know that a “1” won’t exist on both dice? If we know a single prime product exists, can we be sure that others must exist?
(5) What do products with only four factors tell us?
Every product will have “1” and itself as factors, but what if there are only two other options? Take the example of “27”. We are fairly certain that “1” and “27” didn’t multiply to achieve “27” because if “27” existed on a face of a die, we would (likely) see other multiples of “27” in the results. There is one (54), but it seems unlikely that either the other dice is dominated by 2s and 1s, or the “27” just wasn’t rolled in conjunction with the other options. It leaves “9” and “3” as excellent options for dice sides.
(6) What do perfect squares tell us?
The knee jerk reaction here is to assume that a perfect square is created by the multiplication of identical factors. There is something attractive about that symmetry. It is not true in the case of “4” and “9”, and gets even more convoluted in the case of “36”. This assumption, of course, ignores the possibility of pairing the perfect square with a “1”. It is interesting to note that a “4” must be constructed with two 2s if there is no “1” / “4” pairing possible. The same goes for the product of “9”. The existence and placement of a “1” gains importance yet again in this case.
Summary:
If your goal is to study factors and products, allow the probability to slink into the background and remain governed by intuition. Focus on the composition of the numbers and the characteristics of primes, perfect squares, and common factors.
If your goal is to study probability, use the factors as a vehicle to have conversations of likelihood. Encourage formality to justify conjectures of probability, and live in the very real tension between experimental and theoretical probability.
The task doesn’t throw out the representations of classical probability or the theorems of factors and products. Rather, it opens a space for students to act on both topics in ways that emerge as necessary at the time.
While I don’t tend to give out solutions to problems, I feel like teachers are more likely to use this task if they know the composition of the dice that created the 100 trials. (Yes, I created the dice and actually rolled them 100 times).
Dice 1: 2, 3, 1, 6, 4, 6
Dice 2: 9, 10, 5, 3, 2, 2
My suggestion is to never reveal this composition to your students. I know you, as a teacher, probably have this weird “master of math” vibe and most likely feel incredibly insecure in the uncertainty of all of this–but your students haven’t earned the right to be this unnaturally uptight about their work yet.
As far as classroom assessment, I like to collect viable solutions complete with justification. I attempt to focus on the process of establishing the mathematics, and a grand reveal of the right answer bankrupts that immediately.
Happy rolling.
NatBanting
*tongue-in-cheek reference to the idea of “flipped classrooms” of which I remain extremely skeptical.
2 replies on “100 Rolls Task”
I had it except that I thought the 2nd die had two tens instead of two twos. (I wonder if mine were just as likely.) I didn't need the answer but a file with the numbers to be played with would have helped. I typed them all into a spreadsheet. Here: https://docs.google.com/spreadsheets/d/1EMknZYgz55gq5eyqIDFvfUr_RCIACDD4hRgRDeU_jGs/edit?usp=sharing
Hello! This post was recommended for The Best of the Math Teacher Blogs 2016: a collection of people's favorite blog posts of the year. We would like to publish an edited volume of the posts at the end of the year and use the money raised toward a scholarship for TMC. Please let us know by responding via http://goo.gl/forms/LLURZ4GOsQ whether or not you grant us permission to include your post. Thank you, Tina and Lani.