My first attempt at animating patterns was published on this blog in 2013. I suppose you can consider this post a long-overdue extension of the thinking there, however with a much-needed bump in production quality. In those old days, I hunched over a whiteboard with a collection of square tiles, creating six-second loops on the (now defunct) social media platform, Vine. Now, thanks largely to Berkeley Everett and his crash course on how to make animations in Keynote, the process has become much more streamlined.
Some quick details about how I implement these in the classroom:
- I start with a static image of a growing pattern. (There are a plethora of these available at visualpatterns.org)
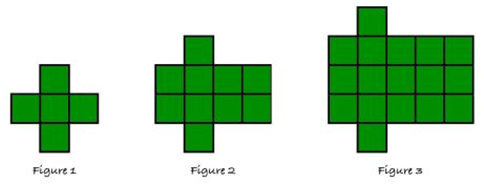
- I usually begin with a linear pattern. I find this to be a comfortable starting point to learn the classroom routine.
- I begin with the prompt: “Describe in words how the pattern is growing”. I am very strict with the constraint that I only want words. From this, all sorts of inventive terminology emerges to describe the sections of the pattern. (e.g., “tail,” “legs,” “strips,” or–my personal favourite–“nubs”).
- After groups share their descriptions of how the pattern is growing, we play the animations. (If a student comes up with a new way to see it, I build that animation for the next time).
- Only then, do we start to describe the growth with algebra through questions like, “What changes and what stays the same?” and “How big is the ____?”
- I find that rapid series of questions are useful for tethering the stage number to the size of certain features in the pattern. How long in Stage 1? How long in Stage 2? How long in Stage 3? How long in Stage 10? etc. What rule are you using to get those lengths so quickly? How long in stage “x”?
- Only after the ways of seeing the pattern have been described using algebra, we manipulate the symbols to see that they all, when fully simplified, result in identical expressions.
These guidelines emerge from multiple influences. Two especially potent inspirations come from Fawn Nguyen, who developed visualpatterns.org and taught me how to slow down and dwell with the visuals, and Dr. Lisa Lunney Borden, who taught me the importance of movement in the teaching and learning of mathematics.
With that preamble established, take these three patterns as a starting point. Each animation shows a different way to “see” the pattern growing, and it is that difference that plays a critical role in building understanding.
NatBanting
One reply on “Animating Quadratic Patterns”
Looking good, Nat! Not sure if you’ve seen Math Is Visual yet, but it’s a passion project where I try to animate mathematics to emerge the conceptual understandings through models and strategies. Check it out at https://mathisvisual.com