I have spent the better part of 2 weeks going over various mathematical relationships in my Grade 10 class. They have been represented as tables of values, arrow diagrams, and sets of ordered pairs. Relationships, both qualitative and quantitative, have been defined, analyzed, and graphed. My focus on graphical literacy has been previously detailed on the blog. See this link for details.
Numerous relationships were handled. Students we required to create a family tree and then represent its branches as a table of values and set of ordered pairs. Throughout the various exercises, the words “input”, “output”, “domain”, and “range” were consistently used. My family tree mapped the connection between a Domain of “Names” to a Range of “Familial Relationship”. Some of my ordered pairs then became:
(Ben, Brother)
(Kevin, Uncle)
(Marla, Cousin)
…
Qualitative relationships eventually gave way to numerical ones. Students spent time looking at discrete data such as temperatures, test scores, and mileage ratings. It was through these exercises that the terms “independent variable” and “dependent variable” became part of the classroom jargon. On the whole, the topic of relations was well received; I knew that the next step was to define a function–a process that has gone poorly for me before.
I have seen several analogies that are designed to explain functions. Each is usually paired with the textbook definition of function– “a special type of relation where each element in the domain is associated with exactly one element in the range” (Foundations and Pre-calculus 10, Pearson, 2010).
1) The Function Machine
This is the overwhelming favourite of math teachers. In the function machine model, the input value (domain element) is placed in some kind of illustrated hopper of the machine. Different portions of the machine contain different operations and the result is an output value (range element) that drops out of the machine. The idea being that if the output was two different numbers, the machine would no longer be functioning. Teachers then stack the “Multiply by 2” machine against the “Add 1” machine to create the “2x + 1” function machine. The proper output values are then reduced to a matching puzzle of the possible machine parts.
This model may create a visual crutch for the computation of ordered pairs, but does not help students decipher between functions and non-functions. I wanted to use a method that would make the students actively create and modify functions.
2) The Promiscuous Range
I have never used this analogy, but a student brought it to me from another math class in my building. In a function, the domain and range are given personalities. The domain elements are faithful to their mates. They are portrayed as hard-working, blue collar citizens. If a relation is a function, each domain value would never dream of having more than one range mate–that is out of character. The range values, however, are more promiscuous. A function still allows a range element to be paired with more than one domain element. Students find all sorts of off-colour words to describe the range element; in the end, a function has faithful domain elements but possibly promiscuous range ones.
3) The Split Decision / Uncertainty Model
This is the model I chose to employ; I felt it could be used as a diagnostic tool for students when presented with a relation. I presented the definition to the students and we analyzed several relations in tables of values. The input values always lead to output values; each ordered pair is presented as a decision. If a certain domain value presents a split decision or uncertainty in the answer, the relation is not a function. If the entry “2” appears twice in the relation, but one time it is mapped to “3” and the other to “4”, the domain entry has created uncertainty. How is one to answer definitely if there are two options? Students took to this immediately.
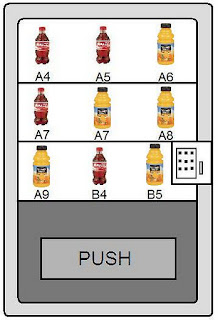
I created this image to further represent the “decision” model.
Students are asked if the vending machine is “functioning”. (You’ll have to excuse the pun). It takes a quick second for students to realize that the input “A7” creates uncertainty. Choosing that input may yield 2 possible outputs–there is no way of knowing.
Functions are practiced for a couple days until I feel it is time to introduce the Vertical Line Test. I do not give them the rule, but rather tell them a story…
The first computer game I ever bought was Sim City 2000. It was somewhat of a cultural phenomenon where the task was to create a functioning city. It gave me my first taste of politics and economics. The game was addictive; hours would melt away as I sat in front of the screen debating whether or not to raise taxes on my figurative citizens. Despite its appeal, there came a point in every game where it was no longer fun to fix run-down neighbourhoods. As seen in the screen shot below, there were several disasters that could be used on your own city. Tornados, hurricanes, and even space monsters were possible. I told my students that we were going to take the same mentality into our study of graphing functions.
I brought up a blank Geogebra file on the IWB and created a blank Table of Values on the adjoining white board. I filled in points one at a time while graphing them as I went. After six or seven, I told the class that the monotony was too much; we were going to begin destroying the function. By themselves, each student was required to create an ordered pair that would destroy the function. After about two minutes I elicited the responses from the class.
As options came, I graphed them on the IWB. After about five or six, I stopped and asked one question:
What do all of these destructive points have in common?
Discussion ensued. By the end of it, we had coined the Vertical Line Test. Students tested their new theorem on sets of points and continuous functions. They now had linked the fact that two ordered pairs lying directly on top of one another created a split decision. They had linked the algebraic and graphical tests for “functionality”.
Functions are the base of higher mathematics in high school. Grade 11 and Grade 12 courses focus almost exclusively on them. I employed a framework where testing if a relation is a function is an active activity. Creating the space for students to actively create and destroy relationships builds a thorough understanding of the topic at hand.
NatBanting