I am teaching 5 new classes next year. I am trying not to think of it that way; rather, I am taking it one step at a time. Unfortunately, most of these steps need to be taken during my summer vacation. This isn’t the end of the world; I am fairly stationary, and enjoy a mental workout as much as some enjoy time on the beach or in a foreign shopping mall. I began my massive preparation marathon with a unit for Grade 10 Precalculus on factoring. As I dove into the curriculum and textbooks, I found myself actually enjoying the intricacies of the topic…nerdy, I know!
The unit has a very distinct division. Part 1 is a look at numbers and their properties. This examines the relationship between a number, its factors, its multiples, and its relationship to other numbers and their factors and multiples. Part 2 is designed to build skills of factoring trinomials, a far more regimented and abstract topic. A solid base in part 1 will lead to a better understanding of the “rules” for factoring polynomials in Part 2.
Numbers are interesting things. I know a lot about them, and still find times when I am amazed at the way their properties interweave. The curriculum calls for the understanding of prime factors, GCF, and LCM. Topics that can be lectured quite simply. It is a shame that students do not get to play with numbers and discover how factors create relationships between them. About a year ago, I stumbled upon a problem that explores the relationships between factors and their products. It provides an interesting juxtaposition on the typical way of learning about prime factors.
Traditionally, factors are taught with trees–clever, branching diagrams to illustrate the “breaking down” of numbers into their constituents. But we can think of factors in two different ways: a number has a unique prime number factorization (this is known as the Fundamental Theorem of Arithmetic), and every composite number has pairs of factors that multiply to give the original. These factors may or may not be prime. For example:
24 = 2*2*2*3
but also…
24
= 1 x 24
= 2 x 12
= 3 x 8
= 4 x 6
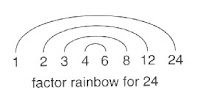
These are the two concepts of factoring at work. More often than not, the focus in school mathematics is on deconstructing. Take 24 and give me its prime factorization. What are the factors of 24? Our textbook uses the rainbow method where pairs of factors are matched with an arc.
Try using the rainbow method for a prime number? What about a perfect square? What about a perfect cube? This activity is an excellent one to do after the odd factors task. Anyway, after I discuss the two basic types of factors, I switch the focus from decomposing to composing, I give the students this task:
Can you construct me a number with 6 factors? How many solutions are possible?
Immediately the question leaves itself up to interpretation. 6 prime factors? Do they have to be unique? What about 6 composite factors? Is that 3 pairs? What if I mix and match prime and composite factors? My response to all of these queries is, “yes”. These questions will help them solve the second half of the problem. When solutions begin to collect on the board, I alter the question a little:
Can you construct me a number with 11 factors? How many solutions are possible?
The same questions emerge, but with a wrinkle. How can you have an odd number of factors in a rainbow? What does this mean? This question takes a while to hammer out. Students can construct a number with 11 prime factors fairly easily, but the composite pairs question is much more difficult. The topic of uniqueness will most likely come up. How many prime factors does 100 have? 2,2,5,5… does that mean 4, or 2? How many pairs of composite factors?
1 and 100
2 and 50
4 and 25
5 and 20
10 and … 10?
so 9 unique factors in total?
This discussion is very valuable. It leads my students toward the special situation of perfect squares–also a curricular outcome. Odd factors is easy to implement with very little logistical pieces, but the user should be warned: this problem has the habit of opening doorways for divergent discussion. Do not be surprised if you find yourself explaining the existence of an infinite amount of primes. The switch of focus from deconstruction to construction allows students to see the intricacies of numbers and their factors. This deeper understanding should also carry into the topics of GCF, LCM, and Polynomial common factors. Teachers may be surprised with the volume that they learn when they subject themselves to a different perspective on a relatively simple concept like factors.
For the record, I believe that the original problem came from the work of Joan Countryman, but I cannot be sure.
NatBanting