I completed school before manipulatives were in vogue. I am still not sure that they are today (where I teach). I know that my department’s manipulatives are locked up in a cupboard. In this Potter-like clandestine state, I didn’t even learn of their existence until the end of the year. I was moving classrooms, and found a pile of algebra tiles that the previous teacher had left behind. I didn’t discover that I had manipulatives available to me until, ironically, I inquired where I could dispose of this rather large supply of algebra tiles. When I opened the doors of the cupboard, my eyes were bombarded with a vibrant display of primary colours; it is the bright reds, blues, and yellows that initially deter high school students from using these instruments. It creates an aura of immaturity and frivolity. They are coloured in such a way that one may expect students to pack their algebra tiles up neatly and proceed to recess or nap time. Kindergarten students play with blocks; algebra deals with “big-kid’ stuff–no use for toys.
Initial impressions aside, the colour of the tiles was not the only thing deterring me from incorporating them into my classroom. It seemed strange to me that someone would try to teach the concept of variability with objects that were horribly static. My “x” block was not “x”, it was a certain area just like the other tiles. There is no way to concretely detail to the students the unknown status of such tiles. After all, aren’t the tiles designed to give a concrete nature to variability? Simply telling the students this defies the very purpose of the tool.
Secondly, I never understood the connection between the tiles and why they represented the values they did. That isn’t completely true, I knew that it was the area of the tile gave it its name. The solution to this problem lies in the way that factoring is introduced to students. It needs to be linked to the factors of numbers, their greatest common factor, multiples, etc. For this geometric tool to be effective, we need to begin to see numbers as geometric bodies. It was twitter that gave me the solution to my 3 hang-ups with algebra tiles; this allowed me to explore some of their interesting uses.
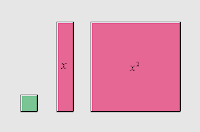
Before we go on, I will introduce the tiles to those who have never seen them. (Chances are they are locked in a cupboard somewhere). There are 3 basic tiles:
1) ‘1’ tile
2) ‘x’ tile
3) ‘x^2’ tile
Pictured above, the tiles get their name from their dimensions; it is essentially a measurement of their area. The shorter dimension has a length of 1, the larger has a length of ‘x’–an unknown. When you create the 3 possible combinations between the 2, you get:
1*1 – The 1 Piece
1*x – The x Piece
x*x – The x^2 Piece
Each piece has an additive inverse (a negative) which is represented by the same dimensions but a different colour. To get more familiar with this tool, go to:
The National Library of Virtual Manipulatives (Utah State University)
The site above has forced me to re-think algebra tiles because it addresses their 3 main flaws:
1) You will notice that the blocks are not brightly coloured. They give off a less childish impression. The layout is sophisticated; this goes a long way for a high school student. I understand that this “flaw” is very superficial, but a first impression goes a long way.
2) The elasticity of the tiles allows me to geometrically and concretely show the idea of variability with the tiles. The site allows me to change the dimensions of the tiles while still retaining the same polynomial expression. The site has a built in slider that can increase the length of ‘x’. The students can see how the polynomial area changes, based on the value of ‘x’. Take the polynomial x^2 + 2x + 1. It is represented below with 2 different values for ‘x’. The polynomial name stays the same, but they represent two very different areas.
This feature sets the virtual manipulatives apart from the physical ones. The SMART board allows those students who are tactile to still physically touch and move the tiles, so this element is not lost either. With the power of computers, the tiles have become variable.
3) The idea of area in the tiles has been addressed by the curriculum renewal in our division. Now trinomial factoring is addressed directly after the topics of GCF and LCM and Prime factors. This allows me to introduce numbers as geometric. What does a “perfect square” look like? Does that mean that numbers like 4, 81, and 144 resemble an actual, geometric square? What shape does 8 take? What about 30? Are all other numbers “rectangular” numbers? Can a number be a “perfect square” and a “rectangular” number? Is a square a rectangle? My students are immersed in a geometric concept of numbers. This allows them to bring geometry into the abstract concept of trinomial factoring.
My biggest trouble as a student was the idea of “completing the square”. My teacher created a clever acronym that has stuck with me to this day, but I never understood what was going on until last week. That is kind of an embarrassing admission from someone who has a degree in mathematics. I learned to complete the square with a set of rules–meaningless rules. Look how algebra tiles addresses the same topic:
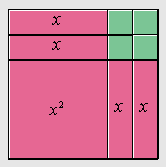
Is this polynomial a “perfect square polynomial”?
A simple re-arrangement of the tiles reveals that this “number” is a “perfect square number”. We just don’t know which perfect square number it represents, that depends on the value of ‘x’? But wait!! Does that mean there are perfect square numbers between the regular ones? Can there be perfect squares with decimals? Try plugging in values for ‘x’. Will any ‘x’ here produce a perfect square? The algebra is becoming an input-output system. Here is the rearrangement:
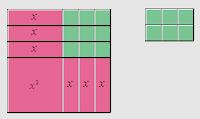
Now, how could we take: x^2 + 6x + 3 and “complete the square”? Well according to my set of rules we first take the middle number (which for some reason is always the ‘x’ number) and divide it by 2, then we square it, then we subtract the constant from that number, then we add and subtract the result to complete the square. This works every time? Why am I adding and subtracting the same number? That is a waste of time! Why do we divide it in 2 first? The series of rules can produce correct answers, but does not produce correct understanding. Let’s look at the same question geometrically: Complete the square.
Here, we see that we physically filled in the pattern until the square was complete. We added 6, so we leave an extra -6 to leave the polynomial unchanged. x^2 + 6x + 3 becomes (x^2 +6x +9) – 6 or (x-3)^2 – 6. We can see the “middle number” as 6, because there are 6 ‘x’ tiles. Why do we divide it is half? Well, we have to split up the tiles between 2 faces of the x^2 tile to make a square. Try other arrangements where you do not divide by 2, what happens? Using this method alongside the rules can shed light on why the rules are what they are. It is also a great test for the teacher to re-learn what they have missed in their schooling.
I have not even introduced the idea of negative tiles; I am still struggling with this myself. Algebra Tiles (especially virtual ones) provide a very powerful learning tool for students (and teachers) when used in the correct way. They can be a gateway to many difficult, and abstract, topics. I am slowly switching camps, and if that means that I have to have recess or nap-time after I am through, both will be welcomed with open arms.
NatBanting