On Brilliance, Relevance, and Impotence: A Classroom Example

Everyone knows that you can’t wish for more wishes, but no one says you can’t wish for more genies.

According to the binding rules of genies (as published by Disney in the 1992 film, Aladdin), there are a few restrictions on what can and cannot be wished for. Probably the most famous restriction is that there is unequivocally no circumstance in which one is permitted to wish for more wishes. This is grouped with three other limitations stating that genies will not kill people, make people fall in love, or revive people from the dead. Other than that, the wishes are limited only by the imagination of the master.

Within these constraints, a wish for more genies is definitely legitimate. That is, there is no questioning whether or not the wish is legal. The question is whether this request should be entertained as brilliant. Is it the work of a jester or a genius?

To establish working definitions for classifications of student actions, I ask you to imagine a classroom of students working on a prompt anticipated to sponsor some type of mathematical activity. In mathematics classrooms, we work within the constraints of curricula and standards; that is our reality. For example, the teacher might anticipate that a specific task might trigger students to compare the sizes of fractions or work with the concept of exponential growth. As learners work within the constraints of a task, every action of a solver results in a series of potential actions as the problem acts back (so to speak). That is, the problem is posed and solved in tandem–the problem changes as it is solved by the solvers. This is an unpredictable process marked with drifts in the nature of the problem under pursuit as students refine and re-define it through their activity. If we conceptualize mathematical activity in this way, a healthy mathematician is one who is able to maintain coherence with the problem environment as it unfolds. 

Defining brilliant, relevant, and impotent.

In this lens, we must distance outselves from (at least) three ways that teachers might assess student actions:

• The first classifies actions based on whether or not they are legal within the task’s constraints. With this classification, impotent actions are strictly those that break the rules. However, this delineation is overly simplistic. For instance, randomly guessing that the solution is 7 is not explicitly outlawed by many questions, but doesn’t seem to contain brilliance.
• The second classifies actions based on whether or not they are correct. However, tasks that sponsor rich mathematical activity involve complex and convoluted lines of argument. Trying to break them down into a series of “correct” steps ignores the idea that problems do not exist in isolation from a solver.
• The third classifies actions based on their novelty. This is perhaps the most dangerous of the three, because even predictable responses are novel to learners as they re-invent problems that are novel to them. It is not fair to compare them to the slew of previous students. On top of that, a well-designed prompt carries with it a degree of predictability. If it didn’t, we (as teachers) would be ignoring our duty to intentionally provide interactions with curriculum outcomes.

Here, I propose definitions of impotent, relevant, and brilliant actions based on the impact they have on the activity itself–on the mathematical knowing. 

Impotent: an action that collapses the need or ability to pursue further activity.

Relevant: an action that results in the circumvention of the intentions of the prompt yet holds potential to pursue further mathematical implications

Brilliant: an action that serves as a catalyst for continued action with the anticipated curricular topics, resulting in new problems and possibilities.

Returning to the movie for a moment, consider the action of the evil Jafar when he used his last wish to become a genie himself. Upon initial inspection, this was a brilliant move. After all, acquiring phenomenal cosmic powers seemed to be the last ingredient he would need to complete his anticipated goal–to rule the known world. However, as any fan of the movie will remember, the status of “genie” comes with restrictions in and of itself. This oversight trivialized a seemingly brilliant wish in the sense that it eliminated further actions toward the intended goal (i.e. Jafar was no longer able to pursue world domination). Impotent actions (such as these) might contain malicious intentions (i.e. “This is stupid” or “I don’t care”), habitual behaviour (i.e. the automatic “I don’t know” reflex), or innocent mishaps (i.e. calculation mistakes or misunderstanding of the goal). The analogy of Jafar seems to be an example of the last.

Into the mathematics class.

For any mathematics class, the intended consequence of the teacher’s actions should be to sponsor mathematical thinking. Our definitions of impotent, relevant, and brilliant–while they are intended to look at student activity–can therefore be applied to the work of teachers. Brilliant teaching keeps students interacting with the goals of a lesson. 

It must be stated that classroom culture plays a huge role in mining brilliance, in keeping students thinking. By this I mean that if the culture is focused on “correct” answers, it can be hard to motivate students to keep thinking once a single solution is offered. This can sterilize even the richest of opportunities by suppressing further activity. Likewise, an argument that might have the potential to offer immediate resolution or deflect thinking can be treated as one with the opportunity to trigger infinite potential. Teaching is a process of arbitrating mathematical activity with an eye to the furtherance of student action. This might result in the manipulation of the environment (by tightening or relaxing constraints) or a shift in perspective of the agent (when a teacher or student is convinced by an unanticipated action). In short, it is the job of the teacher to negotiate impotence, orient relevance, and encourage brilliance. 

Translate this idea into my classroom. On this particular day, we were working thorough the idea of equations and had gone through a series of balance problems like those found here.

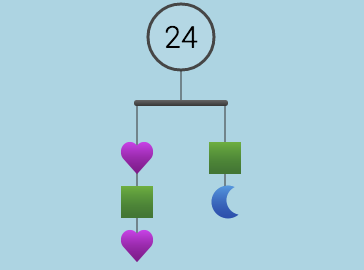
The idea of equality first emerged in our language and we later formalized it into notation. The mobiles were becoming too simple and so I offered a new type of balance problem. In these puzzles, the value of each “weight” (say, “n“) is multiplied by its position away from the fulcrum. In other words, the further from the fulcrum (or balance point), the heavier the weight became (for that equation). A large collection of these can be found here, and the instructions are pictured below. (The reader is encouraged to follow the link and try a few to get the hang of the problems; students took a while to grasp the idea that a single weight can take on different values when compared to different fulcrums). 

A key piece to these puzzles is that the n-puzzle uses the numbers 1 to n exactly once each. After we had solved a few, one student commented that there must be multiple ways to arrange the boxes in any n-puzzle and still get a correct answer. I then isolated the 12-puzzle (pictured below) and offered the following prompt:

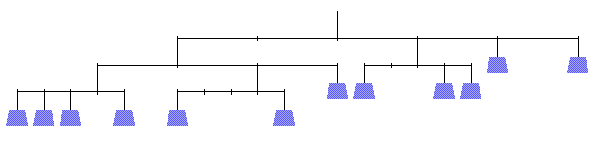
How many possible 12-puzzles can we create?

The students set to work and it did not take long for a group to call me over and explain that they had completed the problem. On their workspace they had created the following a weight organization:

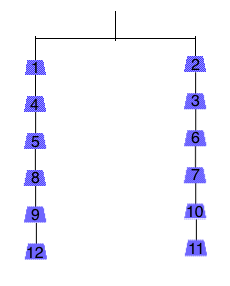Initially, I was shocked at the simplicity of the solution because I did not envision anything like it while I prepared for the class. This initial feeling of shock gave way to intrigue. Something about it seemed brilliant. It fit all of the criteria of the task, and did so in a way that seemed to meld the two types of balance problems together. Ultimately, I felt like this line of reasoning circumvented my intentions with the task. I wanted them to explore multiple, simultaneous instances of equality, but by hanging weights from other weights, they had eliminated the nesting of the equations. 

According to our above definitions, this could be classified as relevant mathematical activity. Therefore, I was forced to either attempt to further this line of thinking (and see what other activity might emerge), or perturb the situation with the intention of orienting activity with the anticipated goals of the task. I am not claiming that there are correct decisions in these moments; I am simply saying that it is a crossroads like these that fuel mathematical activity. These moments are the hard work of teaching.

Perhaps there is an alternate dimension (an upside-down, so to speak) where I choose to amplify this relevant activity and offer something like:

“Great! But how many ways can you hang the weights in this arrangement and still have them balance?”

or maybe I might have moved the entire right-and side one “spot” further away from the fulcrum and asked:

“Is it still possible?”

Perhaps both of these interventions would have sponsored a flurry of mathematical activity, but I was focused on triggering activity with the notion of equality. To be absolutely clear, the activity of the group was not useless. It stood as evidence of mathematical activity, satisfied all parameters of the task, and provided me with important information about their current understanding of equality. Again, there exists a timeline where this thinking is furthered; however, the intention of the task was to work with multiple notions of equality, and this thinking circumvented that. The reality of teaching in a curriculum-based system is that we are responsible for intentionally sponsoring interactions with mandated content, but above all, we should make choices to further mathematical activity–to keep thinking going. There is no wrong choice, only anticipations and improvisations occurring all at once in an ephemeral wind storm. I wanted more complex equations to emerge, and, in that moment, I chose to alter the constraints of the problem to create a landscape that (in my observation) would be more conducive for interacting with multiple, nested equations:

How many possible 12-puzzles can we create if we are not allowed to hang weights from weights?

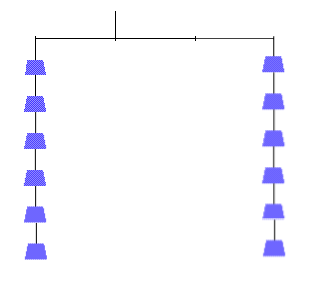
Soon thereafter, another group erupted with a bustle of activity. Out of the noise, I heard one student say, “so it is always possible if we just save 1”. This was their solution:

 

The group explained to me (quite confidently) that there would be an infinite number of ways to create a 12-puzzle because they could arrange the weights 2-12 in any orientation on one side of the fulcrum, calculate the total “weight” by multiplying each by their distance from the fulcrum, and then simply place the last weight (the 1) that many places away from the fulcrum on the opposite side. We called this strategy “the sliding 1”. They went on to explain that this proved that there could be an infinite number of arrangements for each n-puzzle with no weight attached to another weight. 

Take a second to appreciate their activity. They produce a succinct argument that suffices each constraint placed on the task. On top of that, they anticipate extensions and apply their thinking to those cases. In doing so, they construct a theoretical argument based on the notion of equality. They don’t ever concretely draw out the placement for the 1-weight, they use the concept of equality to state that they know it must exist. In doing so, this activity brilliantly brings forth the intentions of the task. 

I added values to the weights and left the group with the specific example to work out, but noticed that their activity had become focused around the calculation of the total value, and no longer with the notion of equality. In an attempt to re-orient their activity, I added a further constraint to the task:

How many possible 12-puzzles with at least two levels of weights can we create if we are not allowed to hang weights from weights?

I anticipated that the group would just move two numbers down a level, place them an adequate distance apart, and then call it quits. Even though I saw this coming, it was the only “teacher move” I could think of in the moment. As the time passed, I grew increasingly curious with what they were doing. Eventually I went over with the assumption that they were stuck. When I asked what was wrong, they told me they were done. They immediately called their solution, “the sliding 2”.

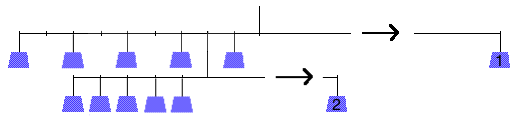
They went on to explain that they dropped all the even numbers down a level and then re-produced “the sliding 1” with the 2-weight as a replacement. They explained how they knew that, because they only moved the even numbers, the result after each multiplication would always be even and therefore could be balanced with a sliding 2. On the top level, the sliding 1 still balanced every possible result. In doing so, the group had extended their theoretical understanding of equality as well as computed the values of a series of equations to place the sliding values. The result of the students’ activity (and the teaching decisions intent on amplifying brilliance) was a solution that was elegantly presented, eloquently defended, and–dare I say–wholly and completely brilliant.

Such evolution of thought evades a playbook of teacher action. There is no diagnosis followed by a surefire treatment for every possible scenario that arises in the midst of mathematical knowing. The action of this group was not a direct result of the task nor the interventions I offered; it emerged an amalgam of the two. The descriptions of impotent, relevant, and brilliant actions are as close I have ever come to describing my decision making process amidst these complex moments of teaching. It is my attempt to offer a framework for how I wade through the density of student thought and attempt to impact student thinking. The descriptions are not flawless, but they are useful (at least, for me).

My hope is that they might assist with the work of teachers as they act to negotiate impotence, orient relevance, and encourage brilliance. 

NatBanting