Billy: “Banting, I have a question for you.”
It was 5-minute break between classes and I was trying to reset the random seating plan, open up the electronic attendance system, and load the image that would serve as a starter for the day’s lesson. During this small window of time, questions are usually about missing binders, requests for future work due to mid-semester holiday plans, or updates on my ever-present pile of grading. In short, I usually do not want to deal with them. Begrudgingly, I obliged.
Billy: “I need a piece of paper and a pen”
This student (affectionately referred to as “Billy”) went on to sketch the graph of a familiar function:
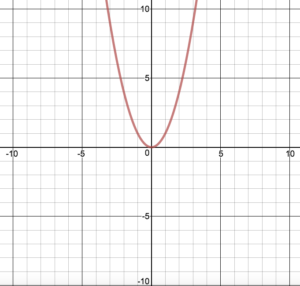
He then went on to explain that he knew that there is an infinite number of solutions to the inequality “inside” the parabola.

and that there is an infinite number of solutions to the inequality “outside” the parabola.
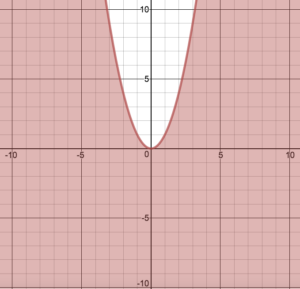
Billy: “But can we say that there are more infinity outside than inside?”
It was now clear that this deserved my attention. In fact, it had grabbed it and under no circumstances was I going to wrestle it back in time to start the next period on time. The great thing about the question was that it appeared obvious, but remained counter-intuitive. This was not the first student to wander into the intricacies of infinity, but I had never heard the question posed in this manner. In that moment, I was at the exact same place as he was: We both “knew” that there was more space outside the parabola when compared to the inside, but were both struggling to find a way to satisfy this intuition. All of this packed into 10 or 15 seconds tops.
Then, a relatively simple argument came to mind: What if we inverted the parabola? There would obviously be extra space that would not be contained “inside” either graph. Further, the two functions are identical, and so contain the same amount of infinity. This then proves that there must be a different degree of infinity contained in the two regions created by the function. Satisfied with the elegance of our solution, we began posing more problems. We drew more parabolas in an attempt to show that the region inside the parabola must be at least 3 times smaller than the region outside.
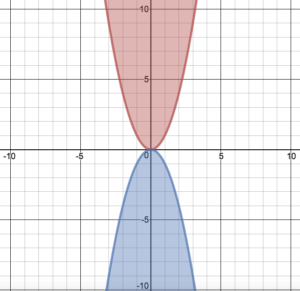
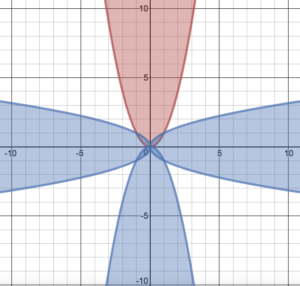
We were in the midst of wondering about a new question (He asked if the vertex of a parabola could be at infinity) when a colleague of mine entered the room. See, Billy is taking two math classes, and this question happened to be a continuance of a conversation from the lesson immediately preceding our class together. His other teacher (who masterfully nurtured this curiosity in the first place) had come to see what had come of her work.
Ms. Neufeld: “I can’t believe you told him!”
I was caught off guard partly because I was still revelling in the simplicity of our argument. Basically, she had shown the pedagogical fortitude to instigate and nurture Billy’s curiosity, and I, in her eyes, had usurped his initiative by providing an answer. And she wasn’t wrong. Class started, and the question dissipated from my consciousness, but during lunch break, I found myself reflecting on what had occurred. What made me lose my pedagogical bearings and douse Billy’s activity? Had I really squelched his process, or did our solution enable him to keep posing new, and interesting, problems? It was as though I was caught in between two states: one where I was pursuing a novel situation, and one where I was fostering the future questions of a student. The former was unscripted and unknown; the latter was calculated and meticulous. Here, I call the former student-ing, and the latter, teacher-ing.
In this particular instance, Ms. Neufeld assumed that I was teacher-ing and was surprised that I had offered a solution to the problem. This is a perfectly reasonable assumption given the mutual influence our past interactions have had on our careers. When I am teacher-ing, I do my best to avoid telling. To me, these two activities (although not disjoint) are not synonymous. However, teaching was the furthest thing from my mind in that moment; I was hooked. Actually, she had done such a fantastic job triggering Billy’s student-ing that it trapped me as well. I was second-hand student-ing.
So when the dust settled, why did this encounter feel important, and what was there to be learned?
First, I think that it is an awful shame that I was able to get so carried away with a problem. Presumedly, this is because, as teachers, we are given little chance to partake in student-ing. This is not surprising given the intense time restraints in which we attempt to influence a fairly strict regimen of concepts. This problem is compounded with years of service providing the opportunity to teach the same credit courses multiple times. Perhaps Billy provided a chance to break with routine, a break I was unable to resist.
Second, I think it is important for students to see us student-ing. Far too often, teachers are assumed to be silos of pre-formed knowledge. However, when done well, teacher-ing is more about fostering activity in students than covering content. This stance of teaching comes with the expectation that students embrace (and occasionally get lost amidst) mathematical activity. This student-ing is a messy, convoluted process that is advanced through an equally precarious teacher-ing. In short, if our teacher-ing calls for intellectual investment from our students, then it can only be strengthened if we model that investment.
(Even unintentionally).
NatBanting
One reply on “Second-hand Student-ing”
[…] He has some deep reflection on teaching in general, and I appreciate his opinions in his post on “Student-ing” and “Teacher-ing”. His blog is extremely valuable to me and other educators because he is truly thoughtful about the […]