This semester I desperately wanted to improve how I taught linear relations to Grade 9 students. I had tried some interesting activities in the past, but lost patience and ended up drilling them with notation and algorithms. I wanted to find a way to show the students that equations were just explanations of patterns. I began compiling different linear patterns and dug in for the long haul.
I stumbled upon a collection of abandoned, square tiles and decided to use them to put students in the center of the pattern making.
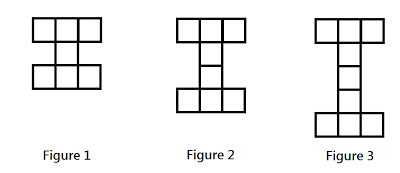
I began the lesson by dividing the class into groups of three. Each group was given a handful of tiles and a sheet with three blank T-Charts on it. To begin the activity, I placed the following pattern on the board:
Students were asked to model the pattern for the next three stages and record how many blocks it took to build each instance. As they were filling out their charts, I went around to each group and asked them to explain the pattern. Most began by saying, “you just add four more each time”. I kept prying at this explanation. I asked them to be more specific.
“You start with a center, and add one on each arm”
“Every time you make the next step, you need to add a tile to each arm”
“The arms have to be as long as the step you are on”
I left after I was sure the groups had made the connection between the four added tiles and increase of four in the table.
Two more patterns were shown, and I repeated the process.
After the third time, students started to be very concise in their wording. They began to tell me what I wanted to hear. It was after the third round that I asked:
“What do all of these patterns have in common?”
They quickly decided that each pattern started with a base and then added a constant amount each time. I (happily) wrote that observation on the board, and handed out a sheet 11″x17″ blank paper to each group. I wanted students to create linear relations with the two newly-defined parts before I formalized their existence as the constant and rate of change.
I explained to the class that each group had three minutes to create their own pattern like the three we had seen so far. The only rules were:
- You must use your blocks to model the first three stages of your pattern.
- You cannot copy or repeat a pattern we have already seen.
- Your pattern must have a starting point and a constant change.
I circulated and heard some great conversations about how they were going to create their patterns. Students would name portions of the pattern “top”, “bottom”, or “middle” and then determine how much it was going to expand each time. This guaranteed that each stage would have a constant change. A wide variety of patterns emerged at a wide variety of skill levels.
My students have used stations before, so they were very familiar with the concept of circulating and completing a T-Chart for each pattern. They had twenty minutes to copy down the first three stages of the pattern, fill out the T-Chart, and decide what the constant change was from every station. They handed in their work at the end of class.
The nice part about the activity was that I could hand back their work the next day when we worked on building equations from the relations. Students had seven great examples to practice building relations. The paper was large enough that the group could easily share. I noticed that more students understood the make-up of equations once they had built their own pattern. They had experienced (and deduced) the existence of a solid piece around which a constant change was occurring.
We went on to discuss other examples of linear relations. Ticket sales at a concert, a taxi cab fare, and Pokemon attack strength. Students got so good at finding the rate of change that filling in the charts was a breeze. It provided a great bridge to graphing and using the relation as an input/output machine.
It’s a very scary thing for a teacher to give up control. Last year, I stood in front of the class and delivered a very good (Read: Twenty-five minute) explanation about how to fill out charts based on patterns. When it came to introducing equations, they got lost and I barreled forward. There is something intangible that occurs when you provide a student with a well-structured task. I have seen the benefits countless times, but still get anxious before I loosen my grip on the class.
This activity now provides an anchor for the learning. I can always refer to the two critical parts of a relation and students will have experienced them first-hand and on their terms.
NatBanting





3 replies on “Relation Stations”
I love this idea so much that I went out and bought my own foam squares. Thanks for sharing.
I’m a new 7th grade sped teacher and I am about to start on constant rate of change. I would like to try this out with my students. Do you have any tips for a sped class?
My one piece of advice would be to have the students talk about the structure of the pattern in words, so it doesn’t just become a pattern that grows in a number of tiles. For instance, the pattern that grows like an “I”. We might talk about the “top,” “bottom,” and “middle” of the pattern. This will help later on as they move toward algebra–having variables represent the sections. Thanks for reading!!