I am frustratingly mathematical. Ask my wife. I see the world as a combination of, in the words of David Berlinski, absolutely elementary mathematics.(AEM). The path of a yo-yo, the tiles in the mall, and the trail of wetness after a bike rides through a puddle are all dissected with simple, mathematical phenomenon. The nice part about AEM is that I can talk about it to almost anyone. People are (vaguely) familiar with graphs, geometric patterns, and circles even if they can’t decipher what practical implications they have on their city block. Unfortunately, people (and students) don’t often want to hear about them–they need to see them.
I can remember the look on my mother’s face when I broke out the silverware to show her that the restaurant table corner was not square. Without a ruler, I showed her that trigonometry allows us to rely on ratio rather than set measurements. As I was in the midst of showing her that the 3-4-5 knife-length rule was breached, the waitress came. Mom was horrified; I was thrilled.
AEM has a visual nature; school mathematics often destroys that nature–reducing it to a simple diagram of a rope hanging from a drainpipe or train chugging its way through the prairie. I am guilty of the same thing in my class. I am a tactile learner so spend the majority of my time teaching with things. Students play with triangles to learn trigonometry and we build models to slope specifications. I often describe problems–good problems–to my students and have them struggle through them. Great learning occurs, but I have robbed them of the ability to find their own problems–the very problems of AEM that exist all around us.
Enter the twitterverse.
I have been watching the work of many educators for a while now. I love the way they use simple, visual elements to create extremely intriguing problems. This past week I was particularly inspired by Timon Piccini (@MrPicc112) and Andrew Stadel (@mr_stadel). They create video problems that not only test the AEM underpinning, but the curiosity and problem solving of the students. It is under this inspiration that I created my first video-based task. It contains a strong visual component and is based on a natural phenomenon that I observed during housework.
Sprinkler Task (V.2) from Nat Banting on Vimeo.
The video shows two takes of me using my “circular” sprinkler on my oddly-shaped piece of lawn. The natural question that came to my mind was, “Where do I place my sprinkler to minimize the amount of water that is wasted?”
The question is broad. The situation is organic. A simple curiosity can be cultivated in a novel way. That is my favorite part of the problem. I will simply play the video for my students. I will pause after the first take and allow students to absorb the situation. Hopefully cynics will point out that the pattern is not circular; this will lead to a great conversation about perspective and spatial reasoning.
I want students to notice that the first pattern touches a corner of the yard. What if the edge of the circle didn’t touch any edge of the yard? Could this possibly be the most efficient watering method?
I will clear up any variables that a good mathematician would. We assume the spray is uniform. We assume that the pressure can be turned up or down to any desired radius. Wasted water is considered water that lands outside of the grass. Wind is not a factor. After our initial conversation, I will re-play the video and see the second case.
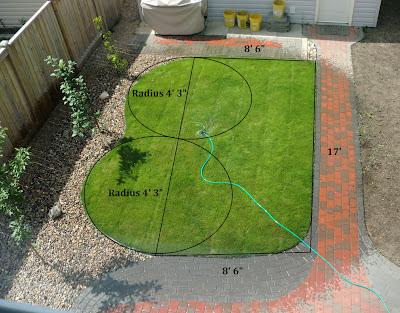
Which one wastes more? Have students discuss. Ask the students what information they need to solve the problem. Measurements will undoubtedly come up. If students are done theorizing with the problem, I provide them with a picture of the yard complete with measurements.
The lawn has been modeled as a rectangle and two semi-circles. What error has occurred? Can we refine the model? (Possibly by placing a quarter circle on the bottom right-hand corner). Do the measurements help you calculate how much water is wasted?
To aid in their work, I created a scale diagram of the yard. I then created three different worksheets–each has a different size scale drawing on it. This creates three unique scales within the classroom. As a group, we will try the first placement together. We’ll draw the sprinkler and create triangles to calculate the distances to the furthest points. The longest of these must be the radius of the sprinkler circle.
I will then send the students out into groups to discover a more efficient placement. If they are going to communicate with one-another, they will have to convert using their scales. For example, “We placed ours 3 inches down and 2 from the left” won’t work if a group has a different scale factor on their diagram.
At the end, I will construct a table of results to see which group indeed maximized the efficiency.
To follow up, I created two other “yards” complete with measurements. I will ask the same question. One involves the possibility of introducing trigonometry and the other has students explore the idea of circumcircles. Both of these diagrams along with three worksheets can be downloaded here.
This is hopefully the first video embodiment of my thinking. Tasks like these not only “real-world”, they cater to multiple learning intelligences. The visual, spatial, kinesthetic, and auditory are all engaged. Some of the best lessons in the classroom mirror experiences that students may have outside the classroom.
NatBanting
3 replies on “Sprinkler Task”
This looks like such a cool problem! I love how simple the problem itself is, yet finding a solution requires much theorizing and uncovering additional layers of information. What's even better is that this problem has a practical "real world" application — minimizing water waste. I've noticed a lot of the kids I teach are impressively conscious about the impact they have on the environment, so I think this aspect of the sprinkler task will draw them in.
I was inspired when I saw this problem, and I'm making a more concerted effort to try and spot other situations that can be turned in an authentic task such as this one. Thanks for sharing this!
Hello, great problem…..would you happen something like this but for Pythgorean Theorem please?….I would like to start doing more of these but need some inspiration!!!
Hey! Sorry for a late reply. One thing I like for this is the “Road Building task” from James Tanton. Written about here: http://natbanting.com/road-building-task/