I have been spending considerable effort looking for situations to “mathematize” in my daily interactions with students. Sadly, upper-level students are so mark and answer focused that they spend little time wondering about emerging problems with me.
This is not the case with my 8-year old friend.
While he was inventing his word problem, he stumbled upon the idea of a middle. Specifically, he told me that four train tracks met in the middle. I quickly asked him if three tracks could also meet in a middle. He responded with an annoyed, “of course”.
A problem was born.
I drew a circle and asked him to find the center. He traced his way around the circumference and made some chords across the shape. When he was satisfied, he placed a dark dot in the interior of the center and smiled. “There”.
I asked him how he knew he was right. He told me that he found the point that was the same distance to each edge. (At this point I thought about asking him how many edges a circle had, but I decided to stay the course.)
I drew a square.
We repeated the process. He used the vertices and tried to find a point that was equidistant. When I asked him if he could use the sides, he discovered that it yielded the same point. He was a little weirded out, but we pressed on.
I drew a rectangle.
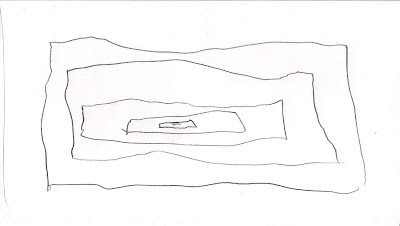
This time his strategy changed. He couldn’t seem to find a way to be the same distance from each side. He placed a point and tried to measure by “pinching” the space with his thumb and index finger. Finally, he erased all his points and traced the perimeter of the shape. He then continued to trace another rectangle inside that one. And another, and another. As he worked, it was obvious that his brain was miles ahead of his hand because the lines got sloppier and sloppier.
When he was done, his rectangle looked like this: (I asked to keep his work)
He proudly explained that tracing his way into the middle of the shape provided a perfect center. I was fascinated by this process, and asked him to apply it to his square.
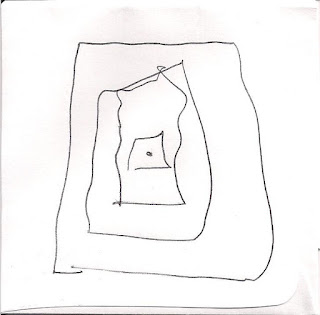
Interesting. I drew a triangle, and he hesitated. I could tell that he thought triangles had no center. Nonetheless, he pressed on:
I was about to add a shape when he stopped.
“Wait”
He went on to explain that a center had to be a dot, and a dot had to be a circle. Using his method, he was creating smaller and smaller rectangles, squares, and triangles. He went on to show me that the dot in the middle of his triangle is just another triangle if “you put it under a microscope”. In fact, he stated that there could never be a center to any shape because the dot would be round and the shape would not be. It could therefore not be the same distance from each side.
I was impressed with his ability to iterate into the infinite. Not only was he constructing geometric knowledge, he was now struggling with the basic structures and how they related to infinity. (Infinity has been his favourite topic for years).
I asked him if a circle has a center.
He waited and responded… “No”.
He explained. Each circle could have a “dot” as a center, but that dot is just a smaller circle, and must have a “smaller dot” as it’s center. Each dot can always get smaller “until it is only a molecule thick”.
And if that is the case, “then there can’t be a middle for anything”. He slumped his shoulders with the weight of this reality.
Here we have a young boy struggling with his personal construction of logico-mathemaitics as juxtaposed to the notation that is meant to describe it. He has been introduced to the formality of “points”, “edges”, and “centers” without ever having the opportunity to construct a deep understanding of what a center is. He is left at a crossroads between his own construction of reality and what the school worksheet tells him.
It is a sad predicament–one created by the burdens of time, curriculum, and the dreaded “test”.
NatBanting

5 replies on “Talking with Children: Shape Centers”
Dang! This should not be a sad predicament. It should be cause for excitement. It sounds to me like he's chewing on ideas. I love that he feels there's no center. He's making his own meaning.
How do tests and worksheets play into this? Are those why he "slumped his shoulders with the weight of this reality"?
@Sue
He is definitely chewing on things. And he really enjoys it.
He became discouraged when he convinced himself there could not be a true center. I think this is because school has told him that circles do, indeed, have one. He had worked hard to make sense of his intricate ideas, and then hit the brick wall of notation.
Tests and worksheets just represent the structure that school imposes upon math. Rules, example, exercises, and exams. In grade 3, he is already well aware of it.
Hmm, can you just suggest that maybe he has a different definition of center, and that one thing real mathematicians do is explore structure based on their starting definitions?
That is exactly what I said. I still felt like I was destroying so much hard work. haha
Your friend has some solid mathematical thinking happening. That's a very astute analysis for someone so young… even for students in my current mathematics classes. If one of SpEd students pointed that out, I would buy the whole class pizza.