Sometime after pyjama time and before bedtime, a math conversation broke out. My wife and I were visiting some good friends, when the topic of a recently purchased board game came up. It was bought at a teaching specialty store and designed to teach addition and subtraction of twos. After examination, I didn’t like the overly symbolic structure, and asked their 5-year old if she wanted to play a math game. She ran and got a piece of paper. When she finally got called up to bed (much later than expected) I took the page and folded it into my back pocket.
Here it is:
Like most educational artifacts, they enliven with the story of their creation. In this case, our “game” made me think of my own classroom and the characteristics that are so often missing. They came so natural to her–a five-year old whose parents just finished telling me that they don’t do much math at home. When my high school students think like kindergarteners, I leave knowing I’ve done my job participating in the action of creating mathematics.
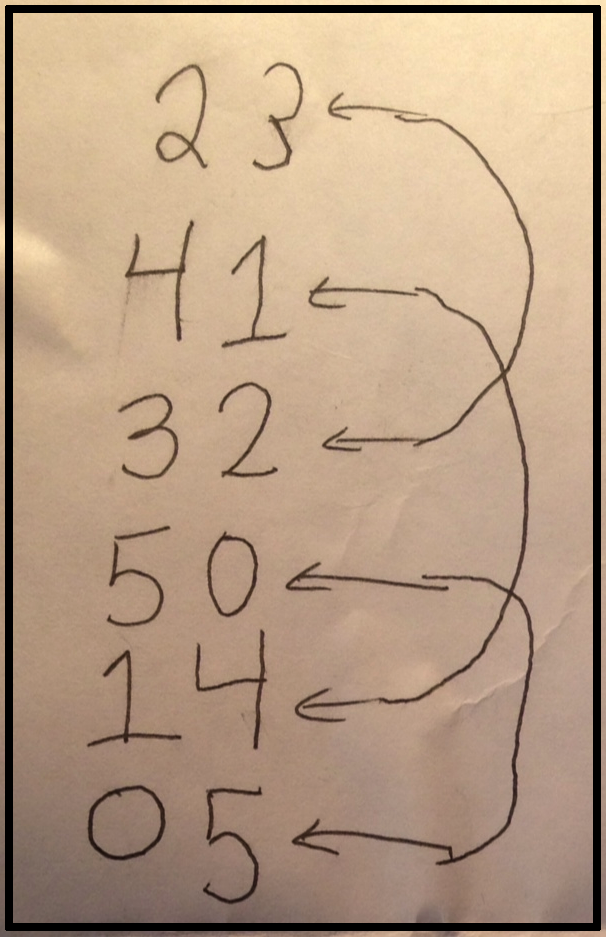
For the sake of clarity, I’ve dissected the image above. Each section carries a mathematical story, one of profound, and innocent, brilliance.
I started by telling her the rules. I gave her a number, and she had to tell me how many more she would need to make five. We went through a few examples (my choices are on the left and she countered with the digits on the right). She started by holding up her hand with all fingers down, and raising the amount that I ‘gave’ her. Then her answer was the number of fingers still down. She counted the raised fingers one by one, but could recognize the ‘down’ fingers almost instantly. During this whole process, I was analyzing her thoughts. So much so that I missed her say, “There are some sames”.
She answered the last question without fingers; she answered it with ‘sames’. She explained (later connecting the arrows) the pattern she saw. Her solution to “0” was a simple mirroring of the solution to “5”.
We then changed the rules. I asked if we could play the same game with 10. She obliged (eagerly) and we began. I decided to start with a large number to see how she would answer. She counted all five on her left hand, and then counted four on her right. Without announcing it, she scribed her answer. She answered all the questions correctly, but later asked if we could change the “7” to an “8”. Then she announced that the answer would be “2”.
Another interesting process was her writing of the numeral “6”. She rotated the page and examined the “9” already on the page. In the end, her second try was the charm. I downplayed the incident; the last thing I wanted was for notation to interfere with the great mathematics going on (which it so often does in high school).
This was the most interesting case in our game of “10”s. I gave her “0”, and she silently thought for a few seconds. Without counting fingers, she gave me a wry smile and told me she was going to use two numbers for the answer. Notice, she didn’t ask, she told. I (naively) assumed she was going to write “10” and was calling that two numbers. Instead, she wrote “5 5”.
She was absolutely correct. The whole point of the game was to decompose 10, and she did just that. She had out-mathed me. I then asked her what the two fives make, and she nonchalantly replied with “10”. I wrote the “10” and also an “=” sign. This was a mistake; I didn’t want any notation. She didn’t notice and we moved on.
This is the coolest part of the page. She wasn’t satisfied once we had finished with our game. She asked, “Is there any more sames?”
When I wrote this on the page, she suggested that she write her name on it. Obviously, credit should be given where credit is due. Then a cool thing happened. She asked if we could make sames of a different number; she wanted to do 12s. I drew two extra fingers on the page (because she didn’t think using toes was a good idea), but she got called to bed before we began.
As she left, she turned and said, “We will do 12s the next time to find the sames”.
Something about this episode is incredibly desirable–especially to a high school math teacher. The strategies used are so free-form and the persistence contains such an honest agency. To her, the math was playful and pliable. In recognizing and extending the pattern of sames, she showed the curiosity to wonder; in justifying and owning her solutions, she showed the industry to get results.
These two attributes are a potent example for any of my high school students.
NatBanting