Mathematics is the purest form of science, or at least that is what they tell us in university. This ideology carries over into the school staff; it wasn’t long until another member of the staff referred to me as a “math guy”. As much as this label is also self-imposed, I still struggle to understand what it means. The labels “english guy”, “phys-ed guy”, and “science guy” all persist within the building as well, but there is something that about the title of “math guy” that gets me.
My friends and family quickly shunt all calculations to me when needed. When I ask then to justify why I must calculate the tax or tip, they simply reply that I am a “math guy”. The public’s perception of mathematics is basic arithmetic. I am a “math guy” therefore I am a human computer. In actual fact, I am no such thing; I have never been excellent with those types of calculations. Math has an aura of exactness about it. It is designed to calculate ideal situations with pinpoint accuracy. This image is also at the heart of the Math Wars. Traditionalists believe that the focus belongs on computation–the need for efficient and correct procedures. The reform side values the very diverse process of doing mathematics. This is not the topic today, and so I will digress, but it would be interesting to see someone who believes fluency is the highest aim of math class struggle with the wiggle room probability and statistics afford.
When setting my classroom up last week, I found a package of wooden dice. They were crudely painted and obviously bought in large numbers. Almost by accident, I opened up a can of worms I never wanted to; I wondered if these poorly constructed dice could possibly be fair. It was not long until I had university textbooks, a generous amount of scratch work on scrap paper, and a book by Joseph Mazur out to help me make my decision. The activity only reinforced the beauty of mathematics.
In an ideal world, if I rolled the die 6 times, each number would appear exactly once. If I rolled it 60 times, each would appear 10 times. In essence, I am calculating the expected number of times that each side should show up if a dice is tossed “n” times. Let’s say I toss the dice 100 times (n=100) then I would expect each side to turn up 16.67 times. Immediately we see the “nearly” creeping into the math. I can’t possibly roll a “3” 16.67 times; each frequency must be a whole number. But in statistics, this is acceptable. The question now becomes:
How many times would a certain number have to appear for me to declare the dice “unfair”?
Certainly, even the most rigid mathematician would not call a dice unfair because a “4” was rolled 18 times in 100, when it should have been rolled 16.67? What about 19, 20, 21, 22? 30? As the process continues, the inexactness of being a “math guy” begins to shine through. Keep in mind, there are very strict laws and formulae that govern the chances of rolling a specific number, but they still only give us chances.
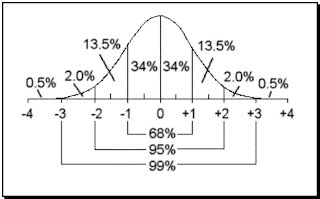
Many of us are familiar with the normal curve shown below. Although rolling a dice is a discrete event (meaning it can be separated into trials) and the curve is based on continuous data, we can still approximate percentages with it.
First we need the mean (average) and standard deviation (distribution from the mean) to calculate values. If ‘n’ is the number of times you roll the dice, ‘p’ is the probability of rolling a specific value, and ‘q’ is the probability of not rolling that value:
Mean = n*p
StDev = Sqrt(n*p*q)
In this case, the mean amount of times we expect to see a value is 16.67, and the standard deviation is 3.73. We use this data to calculate probabilities that a certain number of rolls would occur on a fair dice. I will not go into the calculation of Z-scores and the curve, but any basic statistics book would include that. You can find the table I used to calculate the probabilities here.
It turns out that 95% of the time the frequency will be between 9.21 and 24.1, and 68% of the time the frequency will be between 12.94 and 20.4. The frequency of any number will be greater than 25 only 1.8% if the time, and greater than 20 only 15.39% of the time. These are exact measurements, but the mathematician’s job is more challenging than this:
You still need to decide what percentage is acceptable.
Maybe your mark is 20. Surely 85% is certain enough to judge the dice unfair? Maybe you are pickier and will only pronounce a dice unfair when a side appears 25 times. This is only supposed to happen 1.8% of the time with a fair dice. The ‘nearly’ begins to show.
Now there are other ways to run experiments. You could count the dots on each roll and use that data to make a continuum. In that case the mean number of dots would be 3.5 per roll. How many times would you have to toss the dice, and how far away must the average be to declare the dice unfair with this experiment? It would be a wonderful activity to do with a class of statistics students. It provides them a link between experimental probability and statistics, but, more importantly, teaches them the subjectivity involved in mathematics.
I would introduce them to the normal curve, and then give them each a die. (Some could even be altered to be unfair). I would simply ask to justify if their dice was indeed fair.
It may take a “math guy” to justify the fairness of a dice, but it takes far more than computational fluency to achieve that goal. It just goes to show that sometimes the most innocent wonderings become the richest mathematical experiences. Let’s encourage our students to wonder as well.
NatBanting