The progression followed by most teachers and resources during the study of surface area and volume is identical. Like a intravenous drip, concepts are released gradually to the patients so as to not overdose them with complexity. Begin with the calculation of 2-dimensional areas, and then proceed to the calculation of surface area of familiar prisms. (I say prisms, so a parallel can be drawn to the common structure for finding the volume of said prisms. That is, [area of base x height]). In this way, surface area is conceptualized as nothing more than a dissection of 3-dimensional solids into the now familiar 2-dimensional shapes.
Real-World: An Attack on “Relevance”
**deep breath**
Last week, I caught myself saying something to a pre-service teacher as we planned a Grade 1 lesson for the making of 10s. I asked her,
When she was auspiciously silent, I filled the space with a statement said entirely tongue-in-cheek. It was only upon reflection, that I kicked myself for not being able to shut up and allow her to think. I said,
100 Rolls Task
**Update November 2020. Jamie Mitchell–a fantastic teacher from Ontario, Canada–sent me this google doc that his student prepared to justify her solution. After you wrestle with the prompt for a while, take a second to read this brilliant response!
Most probability resources contain a familiar type of question: the two-dice probability distribution problem.
Often times, it is accompanied with questions concerning the sums of the faces that appear on each dice.
For example:
Background:
On June 15th, my Grade 9 class and I hosted our second annual math fair. What started out as a small idea has grown into a capstone event of their semester. This year, we had 330 elementary school students visit our building to take part in the fair’s activities. Several people (following the hashtag #TDCMathFair2016) commented that they would like to do similar things with their student transitions. This post details the rationale behind the event, how we structured it, what stations we had, and feedback/advice from our exploits.
Mathematics Is: Student Impressions
I have taught the second half of a Math 9 Enriched course for the last three years. The students generally finish two-thirds of the curricular outcomes during the first semester (with an different teacher). This alleviates the perpetual nemesis of time, and leaves me with no excuse to stretch the boundaries of what is possible in a classroom.
MVPs and Fair Teams
**this post was elaborated on in the May 2016 issue of The Variable from the SMTS.
**this game is part of a larger collection of classroom games entitled, 16 Boxes: Ten Numeracy Routines for the Classroom available (for free) at this link.
This is a game that was adapted from a colleague in my department. He can’t quite remember where it came from, but knows there was some influence from his undergraduate days. Nonetheless, he reinvented it to play with his Grade 9s, and this post represents yet another reinvention.
Rationale: Create a game that embeds the skills of adding and subtracting integers into a conceptual decision making structure.
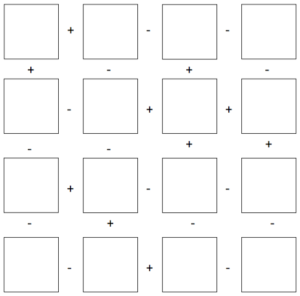
Objective: Insert a set of integers into a 4-by-4 grid so that the sums of the rows and columns is a minimum.
Game Set-up:
All the students need is the game board and the list of sixteen numbers.
Double House Task
Surface area is intuitive. Intuition is a natural hook into curiosity. When you think something might (or should) be the case, it begs the question, why? It just seems as though textbooks haven’t gotten wind of that.
Perusing the surface area chapter of the assigned textbook for my Grade 9 math class offers a steady diet of colourful geometric solids all mashed together (at convenient right angles) in various arrangements. Without fail, the questions ask the same thing:
Find the surface area of…